Wiskundeforum

Je mag niet zomaar een functie kwadrateren, dan wordt het uiteraard een andere...

Negatieve grondtallen van exponentiële functies worden over 't algemeen niet beschouwd bij Reële functies, dus je mag er wel vanuit gaan dat het grondtal telkens positief is. Ik zie niet goed in hoe tot problemen zou leiden...

Het grondtal is 2, niet -2. Er staat

Verder is er iets vreemd aan je manier van vragen stellen, je stelt twee maal iets gelijk aan k(x). Het symbool := betekent "definiëren we als", dus ik weet niet goed wat de vraag precies is.

Klein rekenfoutje nog! deze stap

Bij twijfel, afleiden

Is dit niet gewoon een kwestie van h uit te drukken in functie van x, dan de functie f(x)=x^2*h te beschouwen en daar het maximum van te zoeken?

op=op schreef:De vraag blijft of er een oplossing bestaat waarbij elke deelnemer nooit meer dan één maal dezelfde buren heeft. Dus met abc = cba en ba- = -ab.

Ik geef 't op

Je weet dat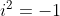
Je weet ook dat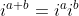
Pas het tweede toe om er dingen uit te halen die je wél kent.

Omdat ik een manier had om telkens een nieuwe permutatie te vinden door telkens voor elke nieuwe permutatie de getallen elkaar laten opvolgen door er telkens +1 meer bij op te tellen en de modulo te nemen, dus bijvoorbeeld voor 5: 1 2 3 4 5 1 3 5 2 4 1 4 2 5 3 1 5 4 3 2 en nog een laatste erbij 1 2 ...

Ja, inderdaad... Hmm dan loopt mijn logica hier vast. Heb je dit gewoon al proberen gevonden of steekt er een formule achter? (Al herken je wel een patroon) Voor drie is het bvb niet mogelijk :/

Wacht, zelfs dan is het niet mogelijk als je als bijkomende eis stelt dat elke visser op elke plaats heeft gezeten.

Probeer maar voor drie vissers en wedstrijden, zelfs dan lukt het niet.

Als je die voorwaarde laat vallen kan het echter wel als het aantal een priemgetal is.

In principe is het hetzelfde als in de fysica op een formaliteit na. Je plakt met andere woorden de twee vectoren aan elkaar, de pijl van de eerste aan de staart van de tweede, en het resultaat is dan van de staart van de eerste naar de pijl van de tweede. De parallellogram methode met andere woorden.

Volgens my is het enkel mogelijk als het aantal vissers en wedstrijden een priemgetal is.

Ik dacht dat 't iets specifiek voor delers van een veelterm was (aangezien er eentje was buitengezet daar waar de term werd gebruikt), ik had er echt nog nooit van gehoord.

Wat je zegt tot nu toe klopt. Het volgende wat je moet doen is je formules voor verwante hoeken voor sin en cos toepassen. Als je je ze niet perfect herinnert, probeer het voor je te zien op de goniometrische cirkel. De bedoeling is om alle k*pi uit de hoeken te halen.