Er zijn 1917 resultaten gevonden
- 27 feb 2021, 13:18
- Forum: Wiskundige puzzels
- Onderwerp: differentiaalvergelijkingen
- Reacties: 1
- Weergaves: 4680
Re: differentiaalvergelijkingen
dx/dt -x=5sin(3t) Is deze differentiaalvergelijking van eerste orde lineair of niet? Leg kort uit. Een lineaire d.v. van de eerste orde heeft de gedaante dx/dt = f(t)·x+g(t). Vergelijk dit eens met de gegeven d.v. en kijk eens of die inderdaad lineair is. Zoek uit hoe je in het algemeen zo’n differ...
- 26 feb 2021, 19:30
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: ONDERZOEKSCOMPETENTIE WISKUNDE
- Reacties: 1
- Weergaves: 4689
Re: ONDERZOEKSCOMPETENTIE WISKUNDE
Neem eens een kijkje op het wiskundeportaal van Wikipedia.
- 04 feb 2021, 18:49
- Forum: Wiskundige puzzels
- Onderwerp: Aantal dozen berekenen
- Reacties: 1
- Weergaves: 3979
Re: Aantal dozen berekenen
Aantal dozen met bal, pet en touw: 2 Aantal dozen met bal en pet: 6 Aantal dozen met pet en touw: 5 Aantal dozen met touw: 5 Aantal dozen met bal en touw: 5 Aantal dozen met bal: 7 Aantal lege dozen: 2 Wat is dus het aantal dozen met alleen een pet? Als 3 van de 4 opgevangen munten Belgisch zijn is ...
- 03 feb 2021, 18:47
- Forum: Praktijkproblemen
- Onderwerp: Oplossen van functies tot inf
- Reacties: 1
- Weergaves: 1691
Re: Oplossen van functies tot inf
Deel teller en noemer door de hoogste macht van x en bepaal aan de hand daarvan de gevraagde limiet.
- 19 dec 2020, 16:25
- Forum: Praktijkproblemen
- Onderwerp: Iets complexer Dan regel van 3
- Reacties: 2
- Weergaves: 2716
Re: Iets complexer Dan regel van 3
Laten we veronderstellen dat een hond van x kg y g aan brokken krijgt, waarbij y = a·x+b. We weten dat y = 150 voor x = 5 en y = 225 voor x = 10. Er geldt dus dat 150 = 5a+b en 225 = 10a+b. Omdat 10a+b = 5a+b+5a en 5a+b = 150 vinden we dat 150+5a = 225, dus 30+a = 45, dus a = 15. Voor b geldt dan da...
- 15 dec 2020, 19:00
- Forum: Analyse & calculus
- Onderwerp: dR/dt vrijmaken
- Reacties: 3
- Weergaves: 4099
Re: dR/dt vrijmaken
Dat is correct. Houd er rekening mee dat X en X, evenals y en Y, 2 verschillende variabelen voorstellen.
Graag gedaan.
- 15 dec 2020, 09:53
- Forum: Analyse & calculus
- Onderwerp: dR/dt vrijmaken
- Reacties: 3
- Weergaves: 4099
Re: dR/dt vrijmaken
Merk op dat (R+dR)²-R² = (R+dR-R)(R+dR+R) = dR(dR+2R) = (dR)²+2RdR. Indien je mag aannemen dat (dR)² verwaarloosbaar is ten opzichte van dR vind je dus dat 2RYdR = Xdt. Wat is dan de volgende stap?
- 13 dec 2020, 15:53
- Forum: Analyse & calculus
- Onderwerp: Variabele vrijmaken in formule met ln
- Reacties: 7
- Weergaves: 5303
Re: Variabele vrijmaken in formule met ln
Bedenk dat 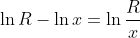 .
.
- 12 dec 2020, 17:47
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: logaritmische functies
- Reacties: 1
- Weergaves: 4832
Re: logaritmische functies
Maak voor het uploaden van je bijlage gebruik van de aangegeven link(s) in viewtopic.php?f=15&t=5039
- 07 dec 2020, 20:51
- Forum: Analyse & calculus
- Onderwerp: Variabele vrijmaken in formule met ln
- Reacties: 7
- Weergaves: 5303
Re: Variabele vrijmaken in formule met ln
Vermenigvuldig links en rechts eens met A·R·B. Hoe komt de formule er dan uit te zien, en wat is dan de volgende stap?
- 07 nov 2020, 13:27
- Forum: Algemeen
- Onderwerp: loodrechte stand van rechten en vlakken
- Reacties: 3
- Weergaves: 6810
- 11 okt 2020, 11:02
- Forum: Praktijkproblemen
- Onderwerp: Functies
- Reacties: 2
- Weergaves: 2271
Re: Functies
Neem eerst eens een aantal termen samen. Het functievoorschrift is dan te herschrijven als f_m(x)=x^2+2(m+1)x-2(m+1) . Maak nu gebruik van het gegeven dat de algemene functie f(x) = ax²+bx+c voor x=-\frac{b}{2a} minimaal is voor a>0 en maximaal voor a<0. Omdat a = 1 vind je in dit geval dus een mini...
- 09 okt 2020, 13:18
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Lineaire vergelijkingen
- Reacties: 9
- Weergaves: 6490
Re: Lineaire vergelijkingen
Hoe is het met de vergelijking 4-12x=1-5(2x-4)? Is het je gelukt om daar de oplossing van te vinden?
- 08 okt 2020, 17:50
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Lineaire vergelijkingen
- Reacties: 9
- Weergaves: 6490
Re: Lineaire vergelijkingen
Begin bij 14-12x=1-5(2x-4) eens met rechts de haakjes weg te werken. De volgende stap is de vergelijking zodanig herschrijven dat alle termen met x links van het gelijkteken komen te staan en de termen zonder x rechts van het gelijkteken. Bij de tweede vergelijking heb je een fout gemaakt. Links moe...
- 06 okt 2020, 08:52
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Hulp nodig bij vergelijking
- Reacties: 2
- Weergaves: 4507
Re: Hulp nodig bij vergelijking
Schrijf de vergelijking eens in de vorm q²+b·q+c = 0 met b = ... en c =... Wat voor soort vergelijking is dit, en hoe los je deze op?