Er zijn 1917 resultaten gevonden
- 04 okt 2020, 14:49
- Forum: Wiskundige puzzels
- Onderwerp: Formule met kromme.
- Reacties: 2
- Weergaves: 4376
Re: Formule met kromme.
Voor de parabool y = ax²+bx+c vind je de top (p,q) door ax²+bx+c = a(x-p)x²+q te stellen. Je vindt dan dat 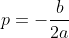 en
en 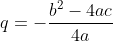 .
.
- 01 okt 2020, 18:52
- Forum: Analyse & calculus
- Onderwerp: Limit van een breuk
- Reacties: 9
- Weergaves: 7370
Re: Limit van een breuk
Een andere vraag: Er staat in dat hoofdstuk ook: Functies van de vorm f (x) = a^{x} voor a > 0 heten exponentiële functies. Is y=\left ( \frac{1}{4} \right )^{x} dan geen exponentiële functie ? Mvgr. Jawel, want ¼>0. Laten we de definitie eens wat helderder formuleren: Functies van de vorm f (x) = ...
- 27 sep 2020, 12:14
- Forum: Analyse & calculus
- Onderwerp: Vereenvoudigen 3e graads functies
- Reacties: 2
- Weergaves: 4386
Re: Vereenvoudigen 3e graads functies
Laten we eens beginnen met x²+x-2. Stel dat dit te ontbinden is als (x+p)(x+q), met p en q geheel, dan moet gelden dat p+q = 1 en p·q = -2. Voor p =2 en q = -1 is aan beide voorwaarden voldaan, dus x²+x-2 = (x+2)(x-1). Om een ontbinding voor x³+2x²-x-2 te vinden zoeken we de delers van -2. Dat zijn ...
- 13 sep 2020, 11:01
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: wat betekent i?
- Reacties: 1
- Weergaves: 5033
Re: wat betekent i?
Het getal i wordt gedefinieerd als een getal met de eigenschap dat i² = -1. Hieruit volgt dan dat i^4=(-1)^2 =1 . Omdat i^4 =1 betekent dit dat i een oplossing is van de vergelijking x^4 =1 . Nu volgt uit x^4 =1 dat x² = 1 of x² = -1. Uit x² = 1 volgt dat x = 1 of x = -1. Uit x² = -1 volgt vanwege h...
- 09 sep 2020, 18:26
- Forum: Algemeen
- Onderwerp: vectoren oef
- Reacties: 3
- Weergaves: 5225
Re: vectoren oef
Weet je wat het duale veelvlak van een regelmatig viervlak is?
- 28 aug 2020, 18:22
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Links/rechts afleidbaar
- Reacties: 3
- Weergaves: 5568
Re: Links/rechts afleidbaar
Voor x<1 is de functie in ieder geval links en rechts afleidbaar en ook afleidbaar. Ga nu eens na wat de situatie is
indien x = 1.
- 26 aug 2020, 18:34
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Links/rechts afleidbaar
- Reacties: 3
- Weergaves: 5568
Re: Links/rechts afleidbaar
Is er ook gegeven wat de functiewaarde is voor x>1? Dat gegeven mis ik hier namelijk.
- 20 jul 2020, 14:37
- Forum: Analyse & calculus
- Onderwerp: Gelijk of ongeveer ?
- Reacties: 3
- Weergaves: 6784
Re: Gelijk of ongeveer ?
De eerste notatie is inderdaad de juiste. Je kunt wel schrijven dathenkoegema schreef: ↑20 jul 2020, 13:18Dus dan zou de conclusie moeten zijn dat:
juist is
en dat
niet juist is.
- 11 jul 2020, 16:54
- Forum: Wiskunde studeren
- Onderwerp: Hogeremachtswortels vereenvoudigen
- Reacties: 3
- Weergaves: 8024
Re: Hogeremachtswortels vereenvoudigen
Graag gedaan.
- 11 jul 2020, 15:17
- Forum: Wiskunde studeren
- Onderwerp: Hogeremachtswortels vereenvoudigen
- Reacties: 3
- Weergaves: 8024
Re: Hogeremachtswortels vereenvoudigen
Jouw uitwerking klopt. Als a een positief getal is geldt altijd dat 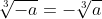 .
.
- 06 jul 2020, 20:46
- Forum: Voortgezet onderwijs / 1ste graad ASO-TSO-BSO
- Onderwerp: oefening veelterm van de vierde graad
- Reacties: 2
- Weergaves: 7113
Re: oefening veelterm van de vierde graad
Omdat A(x) deelbaar is door x²-3 en door 2x+4 en door ax+b betekent dit dat A(x) = (x²-3)(2x+4)(ax+b). Verder is gegeven dat A(x) bij deling door x+1 rest 16 en bij deling door x-1 rest -72 heeft, dus A(x) = (x+1)q(x)+16 en A(x) = (x-1)Q(x)-72, dus (x²-3)(2x+4)(ax+b)= (x+1)q(x)+16 en (x²-3)(2x+4)(ax...
- 31 mei 2020, 21:52
- Forum: Lineaire & abstracte algebra
- Onderwerp: Factoren buiten haakjes
- Reacties: 10
- Weergaves: 11781
Re: Factoren buiten haakjes
Je weet al dat 2(a+3)²+4(a+3) = 2[(a+3)²+2(a+3)], Stel a+3 = p, dan is de uitdrukking te schrijven als 2(p²+2p). Haal nu eens een factor p buiten haakjes en kijk dan eens wat dat oplevert als je weet dat p = a+3.
- 31 mei 2020, 18:16
- Forum: Lineaire & abstracte algebra
- Onderwerp: Factoren buiten haakjes
- Reacties: 10
- Weergaves: 11781
Re: Factoren buiten haakjes
Het gelijke factor wat je nu nog overheid is (a+3), daarom snap ik zelf niet zo goed hoe ze ineens aan de 5 komen. Werk eens even stap voor stap. Je weet dat (a+3)² en 2(a+3) een gemeenschappelijke fac tor a+3 hebben, dus dat betekent dat (a+3)²+2(a+3) = (a+3)(...+...). Wat komt er rechts uiteindel...
- 31 mei 2020, 16:36
- Forum: Lineaire & abstracte algebra
- Onderwerp: Factoren buiten haakjes
- Reacties: 10
- Weergaves: 11781
Re: Factoren buiten haakjes
stel a+3 = p, dan is de uitdrukking te schrijven als 2p²+4p. Welke factor kun je hier buiten haakjes halen, dus wat wordt de ontbinding van 2p²+4p? Wat wordt dan de uiteindelijke ontbinding van 2(a+3)²+4(a+3)?
- 29 mei 2020, 18:04
- Forum: Statistiek & kansrekenen
- Onderwerp: Onbekende knikker
- Reacties: 6
- Weergaves: 7462
Re: Onbekende knikker
In het begin zit er 1 knikker in de zak die groen of geel is. Er wordt vervolgens 1 gele knikker in de zak bijgestopt. Je trekt nu willekeurig 1 knikker uit de zak. Wat is de kans dat de getrokken knikker geel is en de overgebleven knikker groen? Wat is de kans dat de getrokken knikker geel is en de...