Er zijn 1917 resultaten gevonden
- 01 sep 2019, 11:49
- Forum: Analyse & calculus
- Onderwerp: Vraagstuk afgeleide
- Reacties: 3
- Weergaves: 8852
Re: Vraagstuk afgeleide
Stel zeilboot A is de zeilboot in zuidelijke richting en zeilboot B is de zeilboot in oostelijke richting. Na 2 uur heeft zeilboot A dus 12 km in zuidelijke richting afgelegd. Na 4 uur kruist zeilboot B het punt waar zeilboot A 12 km in zuidelijke richting had afgelegd. Merk op dat de snelheden van ...
- 21 aug 2019, 18:42
- Forum: Praktijkproblemen
- Onderwerp: Formule ombouwen
- Reacties: 3
- Weergaves: 5500
Re: Formule ombouwen
Laten we eerst eens 0,00165(X-15) eens uitwerken. Dit geeft: 0,00165(x-15) = 0,00165X-0,02475. De formule is dus te herschrijven als Y=(42,4LG^{0,75}+442X)(0,00165X-0,02475)=0,7293X^2+(0,06996LG^{0,75}-10,9395)X-1,0494LG^{0,75} . Je hebt nu een uitdrukking van de vorm Y = aX²+bX+c. Nu geldt dat aX^2...
- 21 aug 2019, 18:41
- Forum: Praktijkproblemen
- Onderwerp: Formule ombouwen
- Reacties: 3
- Weergaves: 5500
Re: Formule ombouwen
Laten we eerst eens 0,00165(X-15) eens uitwerken. Dit geeft: 0,00165(x-15) = 0,00165X-0,02475. De formule is dus te herschrijven als Y=(42,4LG^{0,75}+442X)(0,00165X-0,02475)=0,7293X^2+(0,06996LG^{0,75}-10,9395)X-1,0494LG^{0,75} . Je hebt nu een uitdrukking van de vorm Y = aX²+bX+c. Nu geldt dat aX^2...
- 26 jul 2019, 15:40
- Forum: Hoger onderwijs - overig
- Onderwerp: Stelsel van vergelijkingen
- Reacties: 7
- Weergaves: 13089
Re: Stelsel van vergelijkingen
x+2y+z = 12
x+3y+2z = 19
6x-5y+2z=-21
Uit de eerste vergelijking volgt: z = -x-2y+12. Vul dit eens in de 2 onderste vergelijkingen in. Je krijgt dan een stelsel van 2 vergelijkingen in x en y waaruit je x en y oplost. Uit de gevonden waarden van x en y volgt dan de te vinden waarde voor z.
x+3y+2z = 19
6x-5y+2z=-21
Uit de eerste vergelijking volgt: z = -x-2y+12. Vul dit eens in de 2 onderste vergelijkingen in. Je krijgt dan een stelsel van 2 vergelijkingen in x en y waaruit je x en y oplost. Uit de gevonden waarden van x en y volgt dan de te vinden waarde voor z.
- 26 jul 2019, 12:55
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Herschrijven als macht van 2
- Reacties: 4
- Weergaves: 6521
Re: Herschrijven als macht van 2
Bedenk dat 2² = 4. Wat wordt dan de uiteindelijke uitkomst?
- 25 jul 2019, 19:23
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Vereenvoudigen wortel van een breuk
- Reacties: 16
- Weergaves: 14812
Re: Vereenvoudigen wortel van een breuk
Merk om te beginnen op dat √12 = 2√3 en √20 = 2√5, dus 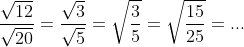 , dus
, dus 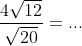
- 25 jul 2019, 17:02
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Vereenvoudigen wortel van een breuk
- Reacties: 16
- Weergaves: 14812
Re: Vereenvoudigen wortel van een breuk
Stel 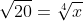 . Links en rechts alles tot de vierde macht verheffen levert dan:
. Links en rechts alles tot de vierde macht verheffen levert dan: ^4=20^2=400) . Merk op dat algemeen geldt dat
. Merk op dat algemeen geldt dat 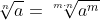 .
.
- 25 jul 2019, 14:42
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Inhoud
- Reacties: 2
- Weergaves: 5100
Re: Inhoud
Ga nog eens na wat de primitieve functie, ofwel stamfunctie, is van -½x+5. Stel P ligt op de rechte y = -½x+5, dan weet je in ieder geval dat P weer te geven is als P(x,-½x+5). Je weet dan ook voor welke x P boven de x-as ligt. Bedenk nu verder dat de cilinder die je krijgt de straal AP en de hoogte...
- 17 jul 2019, 13:37
- Forum: Analyse & calculus
- Onderwerp: Natuurlijke logaritmes
- Reacties: 2
- Weergaves: 7872
Re: Natuurlijke logaritmes
Als ik het goed begrijp wil je A oplossen uit }{A}+1\right)) . Links en rechts verheffen tot de macht e geeft dan:
. Links en rechts verheffen tot de macht e geeft dan: }{A}+1\right)) . Voor zover ik kan zien kan dit alleen numeriek worden opgelost.
. Voor zover ik kan zien kan dit alleen numeriek worden opgelost.
- 13 jul 2019, 12:27
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Logartimische vergelijking
- Reacties: 2
- Weergaves: 5197
Re: Logartimische vergelijking
Merk om te beginnen op dat je de formule van L in die van G kunt invullen. Je weet dat L= -11,31+22,14·O en log(G)= -5,607+ 3,335·log(L), dus log(G)= -5,607+3,335·log(-11,31+22,14·O). Je hebt nu een uitdrukking van de vorm log G = a+b·log(-11,31+22,14·O). Merk op dat a=\log{10^a} , dus \log G=\log{1...
- 01 jul 2019, 17:56
- Forum: Voortgezet onderwijs / 1ste graad ASO-TSO-BSO
- Onderwerp: Juist of fout
- Reacties: 3
- Weergaves: 11106
Re: Juist of fout
Laten we eens kijken naar wat er al gegeven is. Er moet gelden dat x = -x+3x+... We zoeken dus een extra term die opgeteld bij -x en 3x de waarde x oplevert. Optellen van -x en 3x levert: -x+3x = 2x, dus er moet gelden dat x = 2x+... Omdat links x staat betekent dat dat we op de plaats van de puntje...
- 16 jun 2019, 18:57
- Forum: Wiskunde studeren
- Onderwerp: penteract / pentakis dodecahedron
- Reacties: 5
- Weergaves: 13724
Re: penteract / pentakis dodecahedron
Graag gedaan.
- 16 jun 2019, 16:58
- Forum: Wiskunde studeren
- Onderwerp: penteract / pentakis dodecahedron
- Reacties: 5
- Weergaves: 13724
Re: penteract / pentakis dodecahedron
Een penteract is inderdaad vijfdimensionaal, maar een pentakis dodecaëder is een duale vorm van een afgeknotte icosaëder. Een afgeknotte icosaëder is net als zijn duale vorm driedimensionaal.
- 09 jun 2019, 12:34
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Kansrekenen
- Reacties: 3
- Weergaves: 6598
Re: Kansrekenen
Machine X produceert 60% van de dagproductie. Hiervan is 2% onbruikbaar, dus de kans op een onbruikbare sleutel van machine X is 1,2% en de kans op een bruikbare sleutel van machine X is 58,8%. Machine Y produceert 40% van de dagproductie. Hiervan is 0,9 % onbruikbaar, dus de kans op een onbruikbare...
- 02 jun 2019, 15:10
- Forum: Praktijkproblemen
- Onderwerp: Vergelijkingen
- Reacties: 2
- Weergaves: 4634
Re: Vergelijkingen
Schrijf 2√x-x = 1 eens om als 2√x = x+1. Wat krijg je nu voor vergelijking als je eerst links en rechts kwadrateert en vervolgens op nul herleidt? Wat is de oplossing van deze vergelijking? Schrijf 3-\sqrt[3]{x^2}=4 eens om als \sqrt[3]{x^2}=-1 . Wat krijg je nu voor vergelijking als je links en rec...