Er zijn 227 resultaten gevonden
- 14 aug 2011, 09:47
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: rekenkundige en meetkundige rij
- Reacties: 3
- Weergaves: 3151
Re: rekenkundige en meetkundige rij
Dank je safeX, ik had al enkele gevallen genomen waarbij a+b = 2: a= 0.5 en b = 1.5 a = 0.2 en b = 1.8 En inderdaad klopte dat niet. En als a = b = 1 klopt het uiteraard wel. Het probleem met wiskunde-boeken, is dat er fouten in staan (zoals in elk boek, dat is onvermijdelijk). Als je je als leerlin...
- 14 aug 2011, 07:31
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: rekenkundige en meetkundige rij
- Reacties: 3
- Weergaves: 3151
rekenkundige en meetkundige rij
Gegeven B=(a²; ab; b²). De opdracht luidt: aangeven of deze rij rekenkundig of geometrisch is voor gelijk welke a en b. Indien ja, de rede geven. Indien nee: bestaan er waarden voor a en b waardoor de rij rekenkundig of meetkundig wordt. Mijn oplossing: Algemeen: een rij (x;y;z) is rekenkundig als z...
- 06 aug 2011, 16:22
- Forum: Analyse & calculus
- Onderwerp: product van 2 functies afleiden ?
- Reacties: 3
- Weergaves: 3111
Re: product van 2 functies afleiden ?
s^2\cdot4\cdot(3s^2 - 6s + 9)^3(6s - 6) + 2s \cdot(3s^2 - 6s + 9)^4 =(3s^2 - 6s + 9)^3 (4 \cdot s^2 \cdot (6s-6) + 2s(3s^2 - 6s + 9)) =(3s^2 - 6s + 9)^3 (24s^3 - 24s^2+ 6s^3 - 12s^2 + 18s) =(3s^2 - 6s + 9)^3 ( 30s^3 - 36s^2+18s) = 2s(3s^2- 6s + 9)^3(15s^2 - 18s + 9) Zoals altijd: heel erg bedankt, ...
- 06 aug 2011, 15:33
- Forum: Analyse & calculus
- Onderwerp: product van 2 functies afleiden ?
- Reacties: 3
- Weergaves: 3111
product van 2 functies afleiden ?
Goedemiddag, de opgave luidt: "geef de afgeleide van f(x)" met f(x) = s^2 \cdot (3s^2 - 6s + 9)^4 Ik zie daarin het product van 2 functies, namelijk p(x)=s^2 en q(x)=(3s^2 - 6s + 9)^4 Met de formule voor de afgeleide van het product van 2 functies en de kettingregel kom ik tot: s^2\cdot4\cdot(3s^2 -...
- 21 jun 2011, 15:36
- Forum: Analyse & calculus
- Onderwerp: bewijs een ongelijkheid
- Reacties: 15
- Weergaves: 10559
Re: bewijs een ongelijkheid
Merci, SafeX! 
- 21 jun 2011, 15:25
- Forum: Analyse & calculus
- Onderwerp: bewijs een ongelijkheid
- Reacties: 15
- Weergaves: 10559
- 21 jun 2011, 13:53
- Forum: Analyse & calculus
- Onderwerp: bewijs een ongelijkheid
- Reacties: 15
- Weergaves: 10559
Re: bewijs een ongelijkheid
Bedoel je
)
en
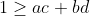
koppelen? Ik versta echt niet waar je heen wil, sorry. Kun je je vraag anders stellen?
en
koppelen? Ik versta echt niet waar je heen wil, sorry. Kun je je vraag anders stellen?
- 21 jun 2011, 11:45
- Forum: Analyse & calculus
- Onderwerp: bewijs een ongelijkheid
- Reacties: 15
- Weergaves: 10559
Re: bewijs een ongelijkheid
Als je uitgaat van (a+c)² + (b+d)² dan krijg je
)
En er is niet gevraagd om dat te bewijzen.
En er is niet gevraagd om dat te bewijzen.
- 21 jun 2011, 10:54
- Forum: Analyse & calculus
- Onderwerp: bewijs een ongelijkheid
- Reacties: 15
- Weergaves: 10559
Re: bewijs een ongelijkheid
Sorry maar ik snap niet waar je heen wilt.
Bedoel je waarom je niet (a+c)² + (b+d)² genomen hebt ipv (a-c)² + (b-d)²?
Bedoel je waarom je niet (a+c)² + (b+d)² genomen hebt ipv (a-c)² + (b-d)²?
- 21 jun 2011, 09:26
- Forum: Analyse & calculus
- Onderwerp: bewijs een ongelijkheid
- Reacties: 15
- Weergaves: 10559
Re: bewijs een ongelijkheid
Inderdaad is jouw manier 'mooier' of 'netter', als ik het zo mag zeggen.
Jouw vraag begrijp ik niet goed.
Jouw vraag begrijp ik niet goed.
- 21 jun 2011, 08:49
- Forum: Analyse & calculus
- Onderwerp: bewijs een ongelijkheid
- Reacties: 15
- Weergaves: 10559
Re: bewijs een ongelijkheid
(a - c)² + (b - d)² is niet negatief, omdat een kwadraat nooit negatief kan zijn, dus de som van 2 kwadraten kan ook niet negatief zijn. Dus hebben we: (a-c)^2 + (b-d)^2 \geq 0 (het geval dat a = c en b = d geeft (a - c)² + (b - d)² = 0) Uitwerken van de merkwaardige producten: a^2 - 2ac + c^2 + b^2...
- 21 jun 2011, 06:08
- Forum: Analyse & calculus
- Onderwerp: bewijs een ongelijkheid
- Reacties: 15
- Weergaves: 10559
bewijs een ongelijkheid
Bewijs: a^2 + b^2 = 1, c^2 + d^2 = 1 \Rightarrow ac + bd \leq 1 Kan iemand een eerste hint geven? Ik vond op internet een mooi bewijs met sinus en cosinus, maar ik denk dat het voor deze opgave de bedoeling is, zonder sin en cos te werken. Dank om niet het volledige bewijs te geven, maar een hint. I...
- 29 mar 2011, 08:59
- Forum: Analyse & calculus
- Onderwerp: Bewijs: irrationale wortels
- Reacties: 10
- Weergaves: 7639
Re: Bewijs: irrationale wortels
Ik moest aantonen dat (2) waar was.
In plaats van (2) af te leiden, heb ik de omgekeerde weg bewandeld: ik ben begonnen bij (2) en ben uitgekomen bij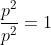 .
.
Daarvoor was de tussenstap nodig die u vermeldt. Nog eens bedankt.
In plaats van (2) af te leiden, heb ik de omgekeerde weg bewandeld: ik ben begonnen bij (2) en ben uitgekomen bij
Daarvoor was de tussenstap nodig die u vermeldt. Nog eens bedankt.
- 28 mar 2011, 20:49
- Forum: Analyse & calculus
- Onderwerp: Bewijs: irrationale wortels
- Reacties: 10
- Weergaves: 7639
Re: Bewijs: irrationale wortels
Stel q = het kleinste getal waarvoor geldt \frac{p}{q} = \sqrt{n} Uit (2) volgt dat er nog een getal q bestaat (namelijk: p-kq met p = nq -kp) en uit (1) volgt dat dit getal (p -kq) kleiner is dan q. Dit is dus in tegenspraak met de aanname dat q het kleinste getal was waarvoor geldt \frac{p}{q} = \...
- 28 mar 2011, 19:07
- Forum: Analyse & calculus
- Onderwerp: Bewijs: irrationale wortels
- Reacties: 10
- Weergaves: 7639
Re: Bewijs: irrationele wortels
fout verbeterd.arno schreef:Opmerking: irrationeel/irrationele moet irrationaal/irrationale zijn.