Onbepaalde integraal

[naomi]

Zet de zaken eens op een rijtje.

∫1/(SQRT(4-64(x)^2))dx

Delen door 64 onder de wortel beteken een factor 8 voor de wortel.

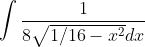
Stel x=1/4cos(t) => dx=...dt

Wat wordt de wortel ... ?

dx=1/4 sin (t) dt
1-cos²(x)=sin^2(x)
Kun je de wortel kwijtraken door met "cos" te vermenigvuldigen?

[SafeX]

Zet de zaken eens op een rijtje.

∫1/(SQRT(4-64(x)^2))dx

Delen door 64 onder de wortel beteken een factor 8 voor de wortel.

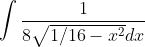
Stel x=1/4cos(t) => dx=...dt

Wat wordt de wortel ... ?

dx=1/4 sin (t) dt
1-cos²(x)=sin^2(x)
Kun je de wortel kwijtraken door met "cos" te vermenigvuldigen?

dx=-1/4sin(t) dt
Je kan onder de wortel met 16 vermenigvuldigen dus voor de wortel door ... ?
En wat is:

?

[naomi]

dus vóór de wortel door 4 delen, en doordat je vermenigvuldigt met 16 komt er onder de wortel 1-cos^2(t) te staan en 1-cos^2(t)=sin^2(x)

[SafeX]

dus vóór de wortel door 4 delen, en doordat je vermenigvuldigt met 16 komt er onder de wortel 1-cos^2(t) te staan en 1-cos^2(t)=sin^2(x)

Heel goed.
En de wortel uit sin²(x) is ...?

[naomi]

∫1/(8/4*sin(t))

[SafeX]

Kijk eens terug, waar blijft dx?

[naomi]

dx=1/4 sin (t) dt

[SafeX]

Dat heb ik verbeterd (ga dat na) en nu moet je wel het geheel opschrijven en verder behandelen.

[naomi]

∫(1/(8/4*sin(t)))*1/4 sin (t) dt

[SafeX]

Ik mis nog iets nl de verbetering.
Daarna kan je toch echt wat vereenvoudigen.

[naomi]

∫(1/(8/4*sin(t)))*-1/4 sin (t) dt
∫((-1/4 sin (t) )/(8/4*sin(t)))dt
∫((-1/4 sin (t) )/(2*sin(t)))dt

[SafeX]

Kan je de integrand echt niet vereenvoudigen?

[naomi]

∫-1/8 dt, maar vraag me af of dit juist is.

[SafeX]

Op zichzelf is dit een legitieme vraag die je je eigenlijk altijd moet stellen.
Laten we aannemen dat het tot zover juist is, wat is dan het antwoord?

[naomi]

dx=-1/4 sin (t) dt
dt=(-4*dx)/sin(t)
∫-1/8 *(-4dx)/sin(t)
∫(1/2/sin(t))dx