Pagina 2 van 3
Re: irrationale functie: schuine asymptoot
Geplaatst: 16 mei 2010, 22:06
door brxpower
Ja ik zie het.
Maar is dit ook (gemakkelijk) algebraisch te benaderen.
Het is wel allemaal leuk om te zien maar kan je deze manier in elk geval toepassen?
Bedankt hoor
Re: irrationale functie: schuine asymptoot
Geplaatst: 16 mei 2010, 22:26
door SafeX
Dit is toch algebraïsch ...
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 12:28
door meneer van Hoesel
SafeX schreef:Dit is toch algebraïsch ...
al 'dit soort methoden' waarbij een formule wordt ingevoerd in een computer of rekenmachine waarbij functies geplot worden, waarden berekend worden tussen een onder en boven grens zijn allen 'numeriek' en 'niet algebraïsch'; dat zijn eigenlijk de meeste computer algorithmen voor het bepalen van nul-punten, afgeleiden en integralen. Kennis van limiten en asymptoten is en blijft belangrijk, want de benaderde grafische weergave kan heel gemakkelijk over verticale asymptoten heen springen en nulpunten kwijt raken als de stap-grootte te groot is.
Er zijn maar heel weinig algebraïsche oplos-methoden, helaas. Op het internet kun je wel gebruik maken van WolframAlpha, die kan nog wel eens de tussen stappen laten zien
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 13:42
door SafeX
Er hoort nog meer bij; zie eerdere posten.
Het 'plaatje' is slechts een illustratie.
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 13:47
door op=op
Om "algebraïsch" aan te tonen dat
=x-1)
een scheve asymptoot is van
=\sqrt{(x-1)^2+9})
moet je laten zien dat
-g(x)) = 0)
.
Om "algebraïsch" aan te tonen dat
=-x+1)
een scheve asymptoot is van
=\sqrt{(x-1)^2+9})
moet je laten zien dat
-h(x)) = 0)
.
Het woord "algebraïsch is hiet onjuist gebruikt. Het moet zijn analytisch.
Analytisch = met limieten (of daarvan afgeleiden zoals integralen en afgeleiden).
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 17:44
door brxpower
Bedankt voor jullie hulp.
Maar de methode van op=op is toch meer een controle methode?
Is er geen andere methode dan die van Safex om tot de SA's van deze functie te komen?
Via de formules van Cauchy bijvoorbeeld?
En het is eigenlijk via deze manier dat ik dit wil doen omdat ik het een mooie manier vind.
y = mx + q is de vgl een schuine asymptoot.
m = lim (x naar +/- oneindig) f(x)/x
q = lim (x naar +/- oneindig) f(x) - mx)
En kan ik alvorens aan al dat rekenwerk te beginnen weten of er een SA is?
Bedankt voor jullie hulp!
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 18:07
door SafeX
Pas die manier (Cauchy (?))eens toe.
Verder heb ik je alles al verteld.
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 18:57
door brxpower
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 19:09
door op=op
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 19:17
door brxpower
Bedankt, maar ik heb al enkele keren willen duidelijk maken dat ik dit "schatten" wil doen via Cauchy. En dan kan ik inderdaad jouw formules gebruiken om dit te CONTROLEREN maar dat kan ik evengoed grafisch doen. Kan niemand me verder helpen met mijn uitwerking via de formules van Cauchy?
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 19:36
door SafeX
brxpower schreef: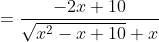
Dit moet eigenlijk zijn:

Deel teller en noemer door x, maar waarom?
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 19:47
door op=op
Mijn methode is geen controlemethode maar een bewijsmethode.
Maar als je Cauchytruc handiger vindt, dan doe je het met Cauchy.
.
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 19:56
door brxpower
zo krijgen we x in de noemer:
weeral limiet gaande van x tot +/- oneindig:
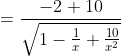
Maar als je hier oneindig invoert krijg je toch 0 in de noemer, niet?
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 19:59
door SafeX
Niet consequent gedeeld, 10 (in de teller) en x (in de noemer).
Re: irrationale functie: schuine asymptoot
Geplaatst: 17 mei 2010, 20:03
door brxpower
SafeX schreef:Niet consequent gedeeld, 10 (in de teller) en x (in de noemer).
Inderdaad.
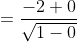
m = 1
q = -2
SA: y = x-2
Klopt niet?