Wiskundeforum

Hallo, ik heb hier een formule die ik moet differentiëren. Ik ben bezig met het kijken naar de invloed van omstandigheden op krekels (bij gebrek aan een beter profielwerkstuk) en nu moet ik de top betalen, want daar zijn de omstandigheden optimaal.. Differntiëren dus maar.
Een deel van de formule (het is een samengestelde, een f(x)+g(x) vorm) heb ik weten te differeniëren. Dit gedeelte hier, daar kom ik niet uit. Het is meer een ik weet niet hoe denk ik zelf dan dat ik echt slecht ben in differentiëren. Het zou kunnen dat het met de quotiëntregel moet, maar dat weet ik dus niet zeker omdat er in de teller geen x staat. De probleemformule staat in de bijlage genaamd 44444444.png.

Heeft weinig met differentiëren te maken, maar als iemand ook zou weten hoe ik het domein van de formule f(lichtintensiteit)=-9,212*0,00625^lichtintensiteit-13,26/(1+Exp(-0,9982*lichtintensiteit+4,125))+17,47 kan bepalen zou ik dat ook willen weten. Je kan in de bijlage genaamd 333333.png zien dat hij aan de rechterkant steeds horizontaler wordt. Hij nadert een bepaald getal op de Y-as, maar ik ben altijd heel slecht geweest met domein en bereik.

Je functie is dus:
?

Wat is de afgeleide van:
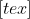
y=a^x{/tex]
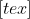
y=e^{ax+b}{/tex]
Verder moet je een quotiënt behandelen.

De horizontale asymptoot kan je vinden door voor x een groot getal te kiezen en dat steeds groter te nemen.
Eigenlijk moet je het dan ook kunnen 'zien'.

De formule is (even je code gepakt en omgebouwd, weet niet uit mijn hoofd hoe het werkt).
-9,212*0,00625^(x) diferentëren is niet veel aan, maar het tweede deel weet ik niet.
Daar ga ik de mist in.

A^x geeft dus ln(A)*A^x
y=e^(ax+b) geeft dus a*e^(ax+b)
Met de quotiënt behandelen bedoel je de quotiëntregel gebruiken?


Die asymptoot kan ik alleen door invullen vinden?
Het staat wel leuk als ik hem algebraïsch kan oplossen, maar ik ben echt heel slecht met asymptoten.

Inderdaad de quotiëntregel met de kettingregel.
En de horizontale asymptoot?

Je zei voor x een flink groot getal nemen, maar zelf zou ik het wat algebraïscher willen, als dat kan.

Maak er een limiet van x->oneindig van...

Ook dat limiet geeft mij problemen.
Dit keer omdat ik met limieten een noob ben.
Blijkbaar vind mijn school het universitaire stof of zo (licht sarcastisch bedoeld), want ik heb er alleen over geleerd in combinatie met differentiëren. En ook dat is niet echt heel veel behandeld.

Ik snap het principe van je limiet naar oneindig wel (oneindig valt niet in te vullen, net als bij differentiëren je langs het probleem komt dat je niet door 0 kan delen en dus een limiet naar 0 moet instellen), maar hoe ik dat algebraïsch zou moeten toepassen op dit probleem...

Dat differentiëren daarbij dacht ik het nog goed te weten hoe het moest, maar moest ik voor de zekerheid navraag doen. Daar zat ik zoals gezegd al met het vermoeden dat ik de quotiëntregel moest gebruiken. Al die regels zijn bij ons vrij uitvoerig behandeld, enige verschil is dat ik bij alle somme altijd een x in de teller had, maar omdat het bij mijn vorige differentiëerprobleem niet zo was, ging ik twijfelen.
Maar limieten, daar weet ik bijna niks van. Ik voel me opeens erg dom.

Bij differenties hebben we ook alleen met limieten uitgelegd gekregen wat differentiatie inhoudt, maar binnen no-time zat ik al weer tussen ingewikkelde constructies en allerlei regeltjes. Daarbij kwam er geen limiet aan te pas.

Vermin schreef:Je zei voor x een flink groot getal nemen, maar zelf zou ik het wat algebraïscher willen, als dat kan.

Ik zei: voor x een groot getal nemen en steeds groter maken (desnoods in gedachten). Dat is ook de basis van de limiet voor x naar oneindig.