Hallo
Ik zit in het 4de secundair met 5 uur wiskunde. Ik heb zojuist een vraagstuk opgekregen. Kan iemand me aub helpen!!!
Iedereen kent waarschijnlijk de legende van het schaakbord van Sessa. De uitvinder vraagt dus een beloning die gaat als volgt; Hij wil 1 graankorrel voor het 1ste vakje, het dubbele voor het 2de, het dubbele daarvan voor het derde, enzoverder.
Nu is de vraag: Hoelang duurt het voor dat de koning de uitvinder heeft beloont.
Deze gegevens heb ik erbij gekregen:
- 1/3 van de aarde is beplant met graan
- 30 hl/ha graankorrels
- 1 liter is 20.000 graankorrels
- de straal van de aarde is 6.300 km
Ik hoop dat dit je niet ontmoedigt zoals velen van mijn klasgenoten en ik zou jullie zeer dankbaar zijn als jullie me konden helpen.
Groetjes Silke
vraagstuk: schaakbord van Sessa
-
filiiiiiip
- Nieuw lid

- Berichten: 22
- Lid geworden op: 01 dec 2010, 18:32
Re: vraagstuk: schaakbord van Sessa
Je moet eerst het aantal korrels bepalen.
Dit kan met een meetkundige rij.
Het standaard voorschrift hiervoor is :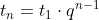
Als je daarin je gegevens invult: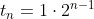
Een schaakbord heeft 8*8=64 hokjes, dus je moet de som van de eerste 64 hokjes van die rij nemen:
}{q-1})
als je je gegevens invult:
}{2-1})
Als je dit uitrekent, heb je al het totaal aantal korrels, maar wat bedoel je met hoe lang? Je hebt toch geen enkel verband met de tijd gekregen?
Dit kan met een meetkundige rij.
Het standaard voorschrift hiervoor is :
Als je daarin je gegevens invult:
Een schaakbord heeft 8*8=64 hokjes, dus je moet de som van de eerste 64 hokjes van die rij nemen:
als je je gegevens invult:
Als je dit uitrekent, heb je al het totaal aantal korrels, maar wat bedoel je met hoe lang? Je hebt toch geen enkel verband met de tijd gekregen?
Re: vraagstuk: schaakbord van Sessa
[1]
Bovenstaande klopt:
Beloning = 1 + 2 + 4 + ... + 2^63 = 2^64 - 1 ~= 2^64
[2]
Bereken vervolgens de jaaroogst = geoogst aantal graankorrels per jaar op aarde, gegeven:
- 1/3 van de aarde is beplant met graan
- 30 hl/ha graankorrels
- 1 liter is 20.000 graankorrels
- de straal van de aarde is 6.300 km
terzijde: hier neem je dus aan dat alle land (29.2% ~= 1/3) met graan bebouwbaar en bebouwd is.
[3]
Deel tenslotte de beloning door de jaaropbrengst, en je hebt het aantal jaren dat nodig is om de beloning te kunnen geven.
Bovenstaande klopt:
Beloning = 1 + 2 + 4 + ... + 2^63 = 2^64 - 1 ~= 2^64
[2]
Bereken vervolgens de jaaroogst = geoogst aantal graankorrels per jaar op aarde, gegeven:
- 1/3 van de aarde is beplant met graan
- 30 hl/ha graankorrels
- 1 liter is 20.000 graankorrels
- de straal van de aarde is 6.300 km
terzijde: hier neem je dus aan dat alle land (29.2% ~= 1/3) met graan bebouwbaar en bebouwd is.
[3]
Deel tenslotte de beloning door de jaaropbrengst, en je hebt het aantal jaren dat nodig is om de beloning te kunnen geven.
