Wiskundeforum

Hallo,

Ik kom niet uit de volgende vraag:

De geboortegewichten van kinderen in een zekere populatie zijn normaal verdeeld met een gemiddelde van 3000 gram en een standaard deviatie gelijk aan 600 gram. Er wordt een random steekproef genomen van 16 pasgeborenen. Wat is de kans dat deze kinderen bij de geboorte gemiddeld zwaarder zijn dan 3075 gram? Deze kans is

a) groter dan 0,5
b) kleiner of gelijk aan 0,5 maar groter dan 0,4
c) kleiner of gelijk aan 0,4 maar groter dan 0,3
d) kleiner of gelijk aan 0,3

Als eerste heb ik een schets gemaakt van het geheel en alle waardes er bij gezet.
Vervolgens gestandaardiseerd met de formule:
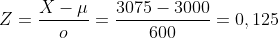
Daarna zoek ik 0,125 op in een tabel voor een normale verdeling => P(Z>0,125) = 0,45

Met dit antwoord zou ik dus kiezen voor B, maar het moet C zijn. Wie kan mij uitleggen waarom het C is?
Alvast bedankt!

thom24 schreef:Hallo,

Ik kom niet uit de volgende vraag:

De geboortegewichten van kinderen in een zekere populatie zijn normaal verdeeld met een gemiddelde van 3000 gram en een standaard deviatie gelijk aan 600 gram. Er wordt een random steekproef genomen van 16 pasgeborenen. Wat is de kans dat deze kinderen bij de geboorte gemiddeld zwaarder zijn dan 3075 gram? Deze kans is

a) groter dan 0,5
b) kleiner of gelijk aan 0,5 maar groter dan 0,4
c) kleiner of gelijk aan 0,4 maar groter dan 0,3
d) kleiner of gelijk aan 0,3

Als eerste heb ik een schets gemaakt van het geheel en alle waardes er bij gezet.
Vervolgens gestandaardiseerd met de formule:
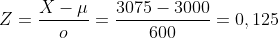
Daarna zoek ik 0,125 op in een tabel voor een normale verdeling => P(Z>0,125) = 0,45

Bedenk dat P(Z>z)= 1-P(Z≤z) = 1-Φ(z) = Φ(-z). Kijk eens of je er zo wel uitkomt.

Waarom geldt: P(Z≤0,125) = 0,45?
Het is toch zo dat je de rechterkant wilt weten?

B lijkt goed ... !

Het gaat hier om de verwachting over het gemiddelde van n = 16 individuen.
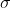
Hiervoor gebruiken we niet de populatie standaard deviatie ( = 600), maar de standard deviation of the sample mean:



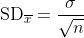
Gebruik deze in je berekening.

Waar kom je dan op uit?


PS: intuïtief: "hoe groter je steekproefomvang n, hoe minder het gemiddelde van die steekproef zal variëren rond het populatiegemiddelde".

thom24 schreef:Waarom geldt: P(Z≤0,125) = 0,45?
Het is toch zo dat je de rechterkant wilt weten?

Ik heb dat inmiddels verwijderd, maar kijk maar eens of je wel goed uitkomt met wat arie aangeeft.

Bedankt voor jullie reacties!

Als ik het advies van arie volg:
SD=600/sqr(16)= 600/4= 150

=>
Z= (3075-3000)/150= 0,5
Opzoeken in de tabel geeft een P van 0,3085

In dit geval is antwoord C dus wel goed!
Wat ik mij alleen nog afvraag is, waarom mag de populatie standaard deviatie ( = 600) niet gebruikt worden? maar de standard deviation of the sample mean?

De standard deviation of the sample mean = de standaardafwijking van een steekproefgemiddelde.
En het gaat hier om de verwachting over het gemiddelde van n = 16 metingen.

Uitspraken/voorspellingen over het geboortegewicht van 1 enkele baby doe je via het populatiegemiddelde en de populatie standaard deviatie.

Maar als je naar een random groep van (in dit geval n=16) baby's kijkt, dan zullen sommige een geboortegewicht onder het gemiddelde hebben, sommige erboven. Het gemiddelde gewicht in zo'n groep zal naar verwachting dichter bij het populatiegemiddelde liggen.
Dus de spreiding van het gemiddelde gewicht in dergelijke groepen (van elk 16 baby's) zal ook minder zijn dan de spreiding van de gewichten van individuele baby's.
En die spreiding wordt gegeven door de standaard deviation of the sample mean.

Voor uitspraken over de grootte van zo'n gemiddelde (zoals in dit geval: "Wat is de kans dat deze kinderen bij de geboorte gemiddeld zwaarder zijn dan 3075 gram?") gebruik je dus ook deze standaard deviatie.

Wordt het hiermee al wat duidelijker?

Hartstikke bedankt! Ik denk dat ik het begrijp. Als ik zou willen weten wat de kans is dat één baby een geboortegewicht had van 3075 gram of meer, dan was mijn 1e berekening dus correct?

Klopt.

Je kan dat ook zien als een steekproef van n = 1, en dan is



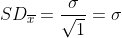
en zo valt alles weer samen.