Pagina 1 van 1
inverse functie
Geplaatst: 15 nov 2019, 17:47
door Steinbach
Verklaar : de inverse functie van \(y=b.a^{x}\) is \(y=^{a}\log (\frac{x}{b})\)
De inverse functie van \(a^{x} = ^{a}\log x\)
Ik weet niet goed wat ik met de \(b\) moet aanvangen ?
Re: inverse functie
Geplaatst: 15 nov 2019, 19:43
door arno
Verwissel in het oorspronkelijke voorschrift eens x en y en herschrijf wat je dan krijgt eens als y = ...
Gebruik het gelijkteken = alleen om een gelijkheid tussen 2 wiskundige objecten weer te geven. Schrijf dus:
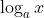
is de inverse van
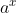
.
Re: inverse functie
Geplaatst: 16 nov 2019, 00:23
door Steinbach
Verwisselen van \(x\) en \(y\)
\(x=b.a^{y}\)
\(\frac{x}{b}=a^{y}\)
\(\log _{a}(\frac{x}{b})=y\)
Hartelijk dank voor je hulp arno.
Re: inverse functie
Geplaatst: 16 nov 2019, 13:15
door arno
Steinbach schreef: ↑16 nov 2019, 00:23
Verwisselen van
\(x\) en
\(y\)
\(x=b.a^{y}\)
\(\frac{x}{b}=a^{y}\)
\(\log _{a}(\frac{x}{b})=y\)
Hartelijk dank voor je hulp arno.
Graag gedaan.
