Rekenregels wortels...

door **Melissa** » 06 Jan 2008, 22:25

Hallo, ik heb altijd problemen met het rekenen met wortels.

Kan iemand mij laten zien waarom het volgende klopt;
1. $sqrt{\frac{1}{10}}=\frac{1}{10}sqrt10$
2. $sqrt10(\frac{1}{10}sqrt10-\frac{3}{10}{i}sqrt10)=1-3i$

Volgende berekening kom ik ook niet uit;
$cos\phi=\frac{1}{10}sqrt10$
$sin2\phi=-\frac{6}{10}$
$sin2\phi=2\cdot\frac{1}{10}sqrt10{\cdot}sin\phi$
$sin\phi=-\frac{3}{10}sqrt10$
Begrijp de berekening niet!
$-\frac{6}{10} / 2 = -\frac{3}{10}$ ok..
maar $-\frac{3}{10} {/} \frac{1}{10}sqrt10=-\frac{3}{10}sqrt10$ ??

door **SafeX** » 06 Jan 2008, 22:44

$\sqrt{\frac{1}{10}}=\frac{1}{10}\sqrt{10}$ Is dit een vraag?

Natuurlijk is:
$\sqrt{\frac{1}{10}}*\sqrt{10}=1$ (eig wortels! ga dat na.)

Je weet (hopelijk): sin(2a)=2sin(a)cos(a) en nu zijn geg het linkerlid en cos(a), dan kan je sin(a) uitrekenen.

De laatste regel:
Eerst teller en noemer met 10 verm, dan heb je 3/sqrt(10), zie boven.

door **Melissa** » 07 Jan 2008, 11:13

De rekenregels zitten er bij mij nog niet volledig in en daarom wilde ik graag dat iemand dmv de rekenregels liet zien waarom bijv. $\sqrt{\frac{1}{10}}=\frac{1}{10}\sqrt{10}$ Heb ik de rekenregels zo goed gebruikt?

Is $\sqrt{\frac{1}{10}}=\frac{1}{10}\sqrt{10}$ omdat $\sqrt{\frac{1\cdot10}{10\cdot10}}=\frac{1}{10}\sqrt{10}$ ?

${\sqrt}\frac{1}{10}\cdot \sqrt10 = (\frac{1}{10})^{\frac{1}{2}}\cdot10^{\frac{1}{2}}=(\frac{1}{10}\cdot10)^{{\frac{1}{2}}+{\frac{1}{2}}}=1$

door **Jampot** » 07 Jan 2008, 11:52

Nee, de laatste regel klopt niet.
Machtverheffen gaat voor vermenigvuldigen.

en de regel $a^p \cdot a^q = a^{p+q}$ geldt alleen als de a's hetzelfde getal zijn. (in jouw geval zijn de a respectievelijk 1/10 en 10)

door **Melissa** » 07 Jan 2008, 13:49

Kun je laten zien hoe het dan moet?

door **Jampot** » 07 Jan 2008, 14:19

door **Melissa** » 07 Jan 2008, 14:53

Jampot schreef: $\frac{1}{10}\sqrt{10} = \sqrt{\frac{1^2}{10^2}} \sqrt{10} = \sqrt{\frac{1}{100}} \sqrt{10} = \sqrt{\frac{10}{100}}=\sqrt{\frac{1}{10}}$

Je hebt nu toch niet $\frac{1}{10}\cdot\sqrt{10}$ gedaan?
Het is al bekend dat het $1$ moet zijn en niet $\sqrt{\frac{1}{10}}$ ? Of mis ik iets?

Ik wil graag de juiste berekening zien voor $\frac{1}{10}\cdot\sqrt10$ omdat ik dat blijkbaar verkeerd heb gedaan.

door **Jampot** » 07 Jan 2008, 15:04

$\sqrt{\frac{1}{10}}*\sqrt{10}=1$
(zie bericht van Safex)
en

$\frac{1}{10}\sqrt{10} = \sqrt{\frac{1^2}{10^2}} \sqrt{10} = \sqrt{\frac{1}{100}} \sqrt{10} = \sqrt{\frac{10}{100}}=\sqrt{\frac{1}{10}}$ ,

Dit volgt uit het stap voor stap volgen van de rekenregels met conclusie:
$\sqrt{\frac{1}{10}} \neq 1$ !

door **SafeX** » 07 Jan 2008, 18:45

@Melissa
Je moet de def van een (vierkants)wortel kennen:
Definitie:
$\sqrt{a}=b$
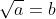
betekent, b is het niet-negatieve getal zo, dat b²=a.
Omdat b²>=0 is volgt a>=0.
Rekenregels (maar(!) twee):
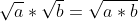
1) $\sqrt{a}*\sqrt{b}=\sqrt{a*b}$ en omgekeerd met a en b niet-neg.
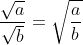
2) $\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$ en omgekeerd met a>=0 en b>0.
De rekenregels volgen (eenvoudig) uit de def.

Verdermoet je onthouden dat het kwadraat van een wortel is het getal onder de wortel, of
$(\sqrt{a})^2=a$
Er is een afspraak om een wortel in de noemer van een breuk voorkomend te vervangen door het getal onder de wortel door teller en noemer met de wortel te vermenigvuldigen.
Dus:
$\sqrt{\frac{1}{10}}=\frac{1}{\sqrt{10}}=\frac{\sqrt{10}}{(\sqrt{10})^2}=\frac{\sqrt{10}}{10}=\frac{1}{10}\sqrt{10}$

Opm: natuurlijk moet je de kwadraten van de getallen 1 t/m 25 kennen en dus ook de wortel daaruit.

Rekenregels wortels...

Rekenregels wortels...

Re: Rekenregels wortels...

Re: Rekenregels wortels...

Re: Rekenregels wortels...

Re: Rekenregels wortels...

Re: Rekenregels wortels...

Re: Rekenregels wortels...

Re: Rekenregels wortels...

Re: Rekenregels wortels...

Wie is er online?

Wie is er online?