Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Dit forum is voor het voortgezetonderwijs (of 2de/3de graad ASO), als je in de bovenbouw zit. We gaan er vanuit dat je een Grafische Rekenmachine hebt.
-
sinek
- Nieuw lid

- Berichten: 13
- Lid geworden op: 17 jun 2006, 13:39
Bericht
door sinek » 25 jun 2006, 23:47
Ik ben nu bezig met het oplossen van een reeks goniometrische bewijzen, en weeral zijn er 2 oefeningen die ik niet krijg opgelost:
Bij de
eerste oefening moet je het volgende bewijzen:
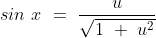
Men zegt er ook het volgende bij:

Bij de
tweede oefening moet je volgende gelijkheid bewijzen:
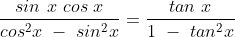
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 26 jun 2006, 10:20
1. Ga uit van tan(x).
De noemer wordt:
}{cos^2(x)}}=)
}}=)
})
Denk er wel aan dat dit niet geldt voor cos(x)=0 => x=Pi/2+k*Pi
2. LINKS: de teller is: 1/2*sin(2x)
de noemer is: cos(2x)
en tan(2x)=???
-
sinek
- Nieuw lid

- Berichten: 13
- Lid geworden op: 17 jun 2006, 13:39
Bericht
door sinek » 26 jun 2006, 14:17
bij die tweede is het linkerlid
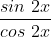
gewoon gelijk aan het rechterlid
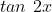
.
T'is simpel maar ik was er nie op gekomen.
Safex, bedankt alvast voor de hulp!
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 26 jun 2006, 23:55
2. OK, mits je eerst links en rechts met 2 vermenigvuldigt.
-
Sjoerd Job
- Vergevorderde

- Berichten: 1144
- Lid geworden op: 21 jan 2006, 15:09
- Locatie: Krimpen aan den IJssel
Bericht
door Sjoerd Job » 29 jun 2006, 10:42
sinek schreef:Ik ben nu bezig met het oplossen van een reeks goniometrische bewijzen, en weeral zijn er 2 oefeningen die ik niet krijg opgelost:
Bij de
eerste oefening moet je het volgende bewijzen:
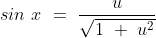
Men zegt er ook het volgende bij:

Bij de
tweede oefening moet je volgende gelijkheid bewijzen:
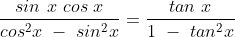
Eerste vergelijking:
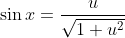
Waarbij
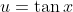
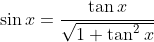
Waarschijnlijk is het handig om de gelijkheid
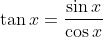
toe te passen...
Waarschijnlijk zul je de volgende regel ook moeten toepassen:
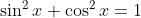
Bij de tweede oefening is het ook veelal handig toepassen van rekenregels... zoek ze op

``Life is complex. It has real and imaginary parts.''
