Hallo,
Ik doe mijn profielwerkstuk Havo over Fibonacci en de gulden snede. Nu zit ik met een probleempje.
Ik heb de formule f(x)=((1+〖√5)〗^x-(1-〖√5)〗^x)/(2^x •√5)
Als je hierin de stap van de reeks invult krijg je het getal wat op die stap hoort.
Nu moet ik uitleggen waar die formule tot stand is gekomen, maar ik heb geen idee hoe dat moet.
Fibonacci differentievergelijking
Re: Fibonacci differentievergelijking
Zie bijvoorbeeld http://www.home.zonnet.nl/LeonardEuler/fibonacci_5a.htm
2 pagina's !
2 pagina's !
Re: Fibonacci differentievergelijking
Bedankt voor de reactie. Maar sorry, hier kom ik niet veel verder mee 
Re: Fibonacci differentievergelijking
De volledige afleiding is inderdaad nogal ingewikkeld, daarom nu stap voor stap.
De rij van Fibonacci is gedefinieerd als
a(n) = a(n-1) + a(n-2)
met 2 beginvoorwaarden:
a(0) = 1
a(1) = 1.
Dit is een tweede-orde recurrente betrekking, omdat er steeds 2 voorgaande waarden
gebruikt worden om de huidige te berekenen.
Bij een eerste-orde recurrente betrekking wordt er slechts 1 voorgaande waarde
gebruikt, bijvoorbeeld:
a(n) = 3 * a(n-1)
met
a(0) = 2.
Als je voor deze betrekking een aantal waarden berekent, dan vind je:
a(1) = 3*a(0) = 3*2 = 6
a(2) = 3*a(1) = 3*6 = 18
a(3) = 3*a(2) = 3*18 = 54
etc.
De algemene oplossing van zo'n eerste-orde betrekking is
a(n) = k * r^n
waarbij k en r constanten.
Om de waarden van k en r te bepalen vullen we dit eerst in in de gegeven betrekking
a(n) = 3 * a(n-1)
dus
k * r^n = 3 * k * r^(n-1)
breng beide termen naar links:
k * r^n - 3 * k * r^(n-1) = 0
haal k en r^(n-1) buiten haakjes:
k * r^(n-1) * [ r - 3 ] = 0
Als k=0 of r=0 zou de hele rij nul worden, dus moet wel gelden:
r - 3 = 0
ofwel
r = 3.
De oplossing heeft dus de vorm
a(n) = k * 3^n
Verder is gegeven dat a(0) = 2, dus:
a(0) = k * 3^0 = k = 2
waardoor:
a(n) = 2 * 3^n
Ga zelf voor een aantal waarden van n na dat dit klopt.
Nu terug naar de rij van Fibonacci:
Neem aan dat
a(n) = k * r^n
een oplossing is voor bepaalde k en r.
Kan je nu zelf eerst de mogelijke waarden van r vinden?
(werk dit uit voor
a(n) = a(n-1) + a(n-2)
op vergelijkbare wijze als voor bovenstaand eerste-orde voorbeeld)
De rij van Fibonacci is gedefinieerd als
a(n) = a(n-1) + a(n-2)
met 2 beginvoorwaarden:
a(0) = 1
a(1) = 1.
Dit is een tweede-orde recurrente betrekking, omdat er steeds 2 voorgaande waarden
gebruikt worden om de huidige te berekenen.
Bij een eerste-orde recurrente betrekking wordt er slechts 1 voorgaande waarde
gebruikt, bijvoorbeeld:
a(n) = 3 * a(n-1)
met
a(0) = 2.
Als je voor deze betrekking een aantal waarden berekent, dan vind je:
a(1) = 3*a(0) = 3*2 = 6
a(2) = 3*a(1) = 3*6 = 18
a(3) = 3*a(2) = 3*18 = 54
etc.
De algemene oplossing van zo'n eerste-orde betrekking is
a(n) = k * r^n
waarbij k en r constanten.
Om de waarden van k en r te bepalen vullen we dit eerst in in de gegeven betrekking
a(n) = 3 * a(n-1)
dus
k * r^n = 3 * k * r^(n-1)
breng beide termen naar links:
k * r^n - 3 * k * r^(n-1) = 0
haal k en r^(n-1) buiten haakjes:
k * r^(n-1) * [ r - 3 ] = 0
Als k=0 of r=0 zou de hele rij nul worden, dus moet wel gelden:
r - 3 = 0
ofwel
r = 3.
De oplossing heeft dus de vorm
a(n) = k * 3^n
Verder is gegeven dat a(0) = 2, dus:
a(0) = k * 3^0 = k = 2
waardoor:
a(n) = 2 * 3^n
Ga zelf voor een aantal waarden van n na dat dit klopt.
Nu terug naar de rij van Fibonacci:
Neem aan dat
a(n) = k * r^n
een oplossing is voor bepaalde k en r.
Kan je nu zelf eerst de mogelijke waarden van r vinden?
(werk dit uit voor
a(n) = a(n-1) + a(n-2)
op vergelijkbare wijze als voor bovenstaand eerste-orde voorbeeld)
Re: Fibonacci differentievergelijking
Bedankt voor de reactie!
Ik kom een heel eind maar op het moment dat ik iets buiten haakjes moet gaan halen snap ik het niet meer.
Ik kom tot k * r^(n-1) + k * r^(n-2) - k * r^n = 0
Ik kom een heel eind maar op het moment dat ik iets buiten haakjes moet gaan halen snap ik het niet meer.
Ik kom tot k * r^(n-1) + k * r^(n-2) - k * r^n = 0
Re: Fibonacci differentievergelijking
Dit gaat goed.
Je hebt
k * r^(n-1) + k * r^(n-2) - k * r^n = 0
ofwel (vermenigvuldig links en rechts met -1):
k * r^n - k * r^(n-1) - k * r^(n-2) = 0
Dit zijn 3 termen.
Weet je om te beginnen hoe je k buiten haakjes haalt?
Vervolgens kunnen we ook r^(n-2) buiten haakjes halen.
Hiervoor moeten we r^n en r^(n-1) iets anders schrijven.
r^n = r^(n-2+2) = r^(n-2) * r^2
Kan je nu ook r^(n-1) schrijven als product van r^(n-2) en nog een factor (welke?) ?
Je hebt
k * r^(n-1) + k * r^(n-2) - k * r^n = 0
ofwel (vermenigvuldig links en rechts met -1):
k * r^n - k * r^(n-1) - k * r^(n-2) = 0
Dit zijn 3 termen.
Weet je om te beginnen hoe je k buiten haakjes haalt?
Vervolgens kunnen we ook r^(n-2) buiten haakjes halen.
Hiervoor moeten we r^n en r^(n-1) iets anders schrijven.
r^n = r^(n-2+2) = r^(n-2) * r^2
Kan je nu ook r^(n-1) schrijven als product van r^(n-2) en nog een factor (welke?) ?
Re: Fibonacci differentievergelijking
k * r^n - k * r^(n-1) - k * r^(n-2) = 0
Als we k buiten haakjes halen krijgen we naar mijn idee dit:
k(r^n - r^(n-1) - r^(n-2)) = 0
En hoe kun je r^(n-1) anders schrijven dan?
Als we k buiten haakjes halen krijgen we naar mijn idee dit:
k(r^n - r^(n-1) - r^(n-2)) = 0
En hoe kun je r^(n-1) anders schrijven dan?
Re: Fibonacci differentievergelijking
Je hebt nu gevonden:
} - r^{(n-2)}) = 0)
voor de machten gebruik je dat
} = x^a \; \cdot \; x^b)
We hadden daarmee al afgeleid:
} = r^{(n-2+2)} = r^{((n-2)+2)} = r^{(n-2)} \cdot r^2)
Op dezelfde manier geldt:
} = r^{(n-1+0)} = r^{(n-1-1+1)} = r^{((n-2)+1)} = r^{(n-2)} \cdot r^1 = r^{(n-2)} \cdot r)
Als je dit allemaal invult in de bovenste vergelijking krijg je
} \cdot r^2 \;-\; r^{(n-2)} \cdot r \;-\; r^{(n-2)}) = 0)
Haal nu de r^(n-2) buiten haakjes net als je met k gedaan hebt.
Wat moet er vervolgens gelden voor k en r zodat de vergelijking gelijk wordt aan nul?
voor de machten gebruik je dat
We hadden daarmee al afgeleid:
Op dezelfde manier geldt:
Als je dit allemaal invult in de bovenste vergelijking krijg je
Haal nu de r^(n-2) buiten haakjes net als je met k gedaan hebt.
Wat moet er vervolgens gelden voor k en r zodat de vergelijking gelijk wordt aan nul?
Re: Fibonacci differentievergelijking
k*(r^(n-2)*r^2 - r^(n-2)*r - r^(n-2))=0
Als je r^(n-2) nu buiten haakjes haalt krijg je(naar mijn idee):
k*r^(n-2)*(r^2-r-1)=0
Als k en r 0 zijn is de vergelijking gelijk aan 0
Als je r^(n-2) nu buiten haakjes haalt krijg je(naar mijn idee):
k*r^(n-2)*(r^2-r-1)=0
Als k en r 0 zijn is de vergelijking gelijk aan 0
Re: Fibonacci differentievergelijking
Klopt, je hebt nu gevonden
}\cdot(r^2-r-1)=0)
Deze vergelijking is nul als ten minste 1 van de 3 factoren nul is:
k=0 OF r^(n-2)=0 OF (r^2-r-1)=0
We wilden de rij van Fibonacci weergeven in een vorm als:
a(n) = k * r^n
Als k=0, dan is de hele rij nul voor elke n, dit klopt niet.
Als r=0, dan is ook de hele rij nul voor elke n, dit klopt ook niet.
Dus als k*r^(n-2)*(r^2*-r*-1)=0 moet zijn EN k niet nul EN r niet nul, dan moet gelden
(r^2 - r - 1) = 0.
Kan je de oplossingen voor r vinden?
Er zijn 2 verschillende oplossingen, noem ze r1 en r2.
De algemene vergelijking voor de rij van Fibonacci wordt dan:
 = k_1 \cdot r_1^n + k_2 \cdot r_2^n)
Maar voordat we verder gaan: wat zijn de waarden van r1 en r2?
Deze vergelijking is nul als ten minste 1 van de 3 factoren nul is:
k=0 OF r^(n-2)=0 OF (r^2-r-1)=0
We wilden de rij van Fibonacci weergeven in een vorm als:
a(n) = k * r^n
Als k=0, dan is de hele rij nul voor elke n, dit klopt niet.
Als r=0, dan is ook de hele rij nul voor elke n, dit klopt ook niet.
Dus als k*r^(n-2)*(r^2*-r*-1)=0 moet zijn EN k niet nul EN r niet nul, dan moet gelden
(r^2 - r - 1) = 0.
Kan je de oplossingen voor r vinden?
Er zijn 2 verschillende oplossingen, noem ze r1 en r2.
De algemene vergelijking voor de rij van Fibonacci wordt dan:
Maar voordat we verder gaan: wat zijn de waarden van r1 en r2?
Re: Fibonacci differentievergelijking
Ah, ik begin het door te krijgen.
(r^2 - r - 1) = 0
A=1
B=-1
C=-1
(-b±√(b^2-4ac))/2a
1+√(-1^2-4*1*-1))/2*1 en 1-√(-1^2-4*1*-1))/2*1
r1=(1+√5)/2=1, 618=φ
r2=(1-√5)/2=-0,618=
dat lijkt naar mijn idee erg op f(x)=((1+〖√5)〗^x-(1-〖√5)〗^x)/(2^x •√5)
(r^2 - r - 1) = 0
A=1
B=-1
C=-1
(-b±√(b^2-4ac))/2a
1+√(-1^2-4*1*-1))/2*1 en 1-√(-1^2-4*1*-1))/2*1
r1=(1+√5)/2=1, 618=φ
r2=(1-√5)/2=-0,618=
dat lijkt naar mijn idee erg op f(x)=((1+〖√5)〗^x-(1-〖√5)〗^x)/(2^x •√5)
Laatst gewijzigd door Janpieter op 30 nov 2010, 20:38, 1 keer totaal gewijzigd.
Re: Fibonacci differentievergelijking
Klopt bijna helemaal: kijk nog eens even goed naar de waarde van r2 (deze is NIET -1.618..., je abc-formule is wel correct)
Goed dat je hier phi (= de waarde van de gulden snede) herkent.
We hebben nu:
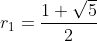
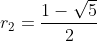
Dit levert in de algemene vergelijking:
 = k_1 \cdot \left( \frac{1+\sqrt{5}}{2} \right)^n + k_2 \cdot \left( \frac{1-\sqrt{5}}{2} \right)^n)
Dit is het algemene gedeelte.
We zoeken nu nog de waarden van k1 en k2.
Eerder hadden we al gezegd: de rij van Fibonacci is gedefinieerd als
a(n) = a(n-1) + a(n-2)
(het algemene gedeelte)
met 2 beginvoorwaarden:
a(0) = 1
a(1) = 1
We gaan nu de beginvoorwaarden invullen in de algemene vergelijking:
voor n=0 levert dit:
 = k_1 \cdot \left( \frac{1+\sqrt{5}}{2} \right)^0 + k_2 \cdot \left( \frac{1-\sqrt{5}}{2} \right)^0)
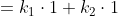
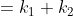
en omdat a(0) = 1:
1 = k1 + k2
dus:
k2 = 1 - k1
Vul dit resultaat al vast in in de algemene vergelijking:
 = k_1 \cdot \left( \frac{1+\sqrt{5}}{2} \right)^n + (1-k_1) \cdot \left( \frac{1-\sqrt{5}}{2} \right)^n)
Nu de 2e beginvoorwaarde invullen:
n=1:
 = 1 = k_1 \cdot \left( \frac{1+\sqrt{5}}{2} \right)^1 + (1-k_1) \cdot \left( \frac{1-\sqrt{5}}{2} \right)^1)
ofwel:
 \cdot \frac{1-\sqrt{5}}{2})
Kan je hieruit k1 oplossen?
Goed dat je hier phi (= de waarde van de gulden snede) herkent.
We hebben nu:
Dit levert in de algemene vergelijking:
Dit is het algemene gedeelte.
We zoeken nu nog de waarden van k1 en k2.
Eerder hadden we al gezegd: de rij van Fibonacci is gedefinieerd als
a(n) = a(n-1) + a(n-2)
(het algemene gedeelte)
met 2 beginvoorwaarden:
a(0) = 1
a(1) = 1
We gaan nu de beginvoorwaarden invullen in de algemene vergelijking:
voor n=0 levert dit:
en omdat a(0) = 1:
1 = k1 + k2
dus:
k2 = 1 - k1
Vul dit resultaat al vast in in de algemene vergelijking:
Nu de 2e beginvoorwaarde invullen:
n=1:
ofwel:
Kan je hieruit k1 oplossen?
Re: Fibonacci differentievergelijking
Oja dat moest -0,618 zijn.
Sorry ik zou niet weten hoe ik hieruit k moet oplossen
Sorry ik zou niet weten hoe ik hieruit k moet oplossen
-
arno
- Vergevorderde
- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Fibonacci differentievergelijking
Begin eens met links en rechts alles met 2 te vermenigvuldigen. Wat levert dat op?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Fibonacci differentievergelijking
Naast wat arno schrijft, lukt het je om uit
 \cdot 2)
ofwel
)
ofwel
 = 1)
x op te lossen?
ofwel
ofwel
x op te lossen?