de stelling van Fermat (voor een bepaalde set getallen)
-
Mathematica
- Vast lid

- Berichten: 41
- Lid geworden op: 29 nov 2009, 12:26
de stelling van Fermat (voor een bepaalde set getallen)
hier heb ik een leuk vraagstukje. Het is eigenlijk een toepassing van de Stelling van Fermat, maar die mag je niet gebruiken om het te bewijzen...
Bewijs dat er geen strikt positieve gehele getallen m en n bestaan waarvoor m³+11³ = n³
Bewijs dat er geen strikt positieve gehele getallen m en n bestaan waarvoor m³+11³ = n³
life is physics, love is chemistry, everything is mathematics...
-
magicsander
- Vast lid

- Berichten: 58
- Lid geworden op: 09 jul 2009, 19:01
Re: de stelling van Fermat (voor een bepaalde set getallen)
Kan je gewoon brute force doen. Net zolang m's uitproberen totdat 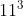 kleiner is dan
kleiner is dan ^2-m^2=2m+1) .
.
EDIT:
dus ff kijken
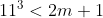
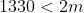
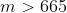
dus m uitproberen voor 1 t/m 666 moet volstaan
groetjes sander
EDIT:
dus ff kijken
dus m uitproberen voor 1 t/m 666 moet volstaan
groetjes sander
-
Mathematica
- Vast lid

- Berichten: 41
- Lid geworden op: 29 nov 2009, 12:26
Re: de stelling van Fermat (voor een bepaalde set getallen)
Zeker dat er geen elegantere manier bestaat? 
De desbetreffende vergelijking is immers een diophantische vergelijking, en ik dacht dat de stelling van fermat voor bepaalde sets getallen daarmee kon worden bewezen
(Ik vind alleen niet hoe dat dan precies moet)
anyway, thnx,
als ik geen andere manier vind, kan ik het zo wel doen...
De desbetreffende vergelijking is immers een diophantische vergelijking, en ik dacht dat de stelling van fermat voor bepaalde sets getallen daarmee kon worden bewezen
(Ik vind alleen niet hoe dat dan precies moet)
anyway, thnx,
als ik geen andere manier vind, kan ik het zo wel doen...
life is physics, love is chemistry, everything is mathematics...
Re: de stelling van Fermat (voor een bepaalde set getallen)
Het kan sneller:
m^3 + 11^3 = n^3
<=>
n^3 - m^3 = 11^3
<=>
(n-m)*(n^2 + nm + m^2) = 11^3
nu zijn n en m beide groter dan nul, dus
(n^2 + nm + m^2) > 0
dus ook
(n-m) > 0
want 11^3 > 0.
Omdat we werken met gehele getallen is (n-m)*(n^2 + nm + m^2) een ontbinding van 11^3, dus
(n-m) = a
met a = 1, 11, 121 of 1331.
uit
(n-m) = a
volgt ook:
n = m+a
en tegelijkertijd geldt voor de andere factor:
(n^2 + nm + m^2) = 11^3 / a
ofwel
n^2 + nm + m^2 - 11^3/a = 0
ofwel:
(m+a)^2 + m(m+a) + m^2 - 11^3/a = 0
m^2 + 2am + a^2 + m^2 + am + m^2 - 11^3/a = 0
3m^2 + 3am + a^2 - 11^3/a = 0
Los hieruit m op voor elk van de 4 mogelijke waarden van a, en ga na dat dit geen geheeltallige oplossing levert voor m^3 + 11^3 = n^3
@magicsander:
kijk nog eens goed naar de begrenzing van m en n (het zijn 3e machten!)
m^3 + 11^3 = n^3
<=>
n^3 - m^3 = 11^3
<=>
(n-m)*(n^2 + nm + m^2) = 11^3
nu zijn n en m beide groter dan nul, dus
(n^2 + nm + m^2) > 0
dus ook
(n-m) > 0
want 11^3 > 0.
Omdat we werken met gehele getallen is (n-m)*(n^2 + nm + m^2) een ontbinding van 11^3, dus
(n-m) = a
met a = 1, 11, 121 of 1331.
uit
(n-m) = a
volgt ook:
n = m+a
en tegelijkertijd geldt voor de andere factor:
(n^2 + nm + m^2) = 11^3 / a
ofwel
n^2 + nm + m^2 - 11^3/a = 0
ofwel:
(m+a)^2 + m(m+a) + m^2 - 11^3/a = 0
m^2 + 2am + a^2 + m^2 + am + m^2 - 11^3/a = 0
3m^2 + 3am + a^2 - 11^3/a = 0
Los hieruit m op voor elk van de 4 mogelijke waarden van a, en ga na dat dit geen geheeltallige oplossing levert voor m^3 + 11^3 = n^3
@magicsander:
kijk nog eens goed naar de begrenzing van m en n (het zijn 3e machten!)
-
Mathematica
- Vast lid

- Berichten: 41
- Lid geworden op: 29 nov 2009, 12:26
Re: de stelling van Fermat (voor een bepaalde set getallen)
Dankje dankje dankje!!!!
duizendmaal dankjewel!







duizendmaal dankjewel!
life is physics, love is chemistry, everything is mathematics...
Re: de stelling van Fermat (voor een bepaalde set getallen)
Schiet me te binnen dat ik ooit eens een erg goede thriller met wiskundige puzzles in heb bekeken.
Genaamd: Fermat's room, echt een aanrader!
Genaamd: Fermat's room, echt een aanrader!
-
Mathematica
- Vast lid

- Berichten: 41
- Lid geworden op: 29 nov 2009, 12:26
Re: de stelling van Fermat (voor een bepaalde set getallen)
nice...
is dat niet zo een film die qua verhaal een beetje lijkt op 'tien kleine negertjes' van Agatha Christie?
een groep mensen die is opgesloten samen met een moordenaar, en dan uiteindelijk elkaar allemaal vermoorden omdat ze elkaar ervan verdenken de moordenaar te zijn, of zoiets... ik weet het niet exact, maar ik geloof dat het zoiets was...
Ik zou die wel eens willen zien
een andere leuke film met wiskunde in is 'The Oxford Murders'...
is dat niet zo een film die qua verhaal een beetje lijkt op 'tien kleine negertjes' van Agatha Christie?
een groep mensen die is opgesloten samen met een moordenaar, en dan uiteindelijk elkaar allemaal vermoorden omdat ze elkaar ervan verdenken de moordenaar te zijn, of zoiets... ik weet het niet exact, maar ik geloof dat het zoiets was...
Ik zou die wel eens willen zien
een andere leuke film met wiskunde in is 'The Oxford Murders'...
life is physics, love is chemistry, everything is mathematics...
Re: de stelling van Fermat (voor een bepaalde set getallen)
Je kan dit evt. ook met de GR oplossen; y^3=11^3+x^3. y=(11^3+x^3)^(1/3). Nu reken je met reële x. Natuurlijke x kan je ervan maken door int(x) te gebruiken. Die rond getallen naar natuurlijke af naar beneden. vb: int(9.6)=9, int(-9.6)=-10. Dus y=(11^3+(int(x)^3)^(1/3). Je kan het bereik van inperken tot 0≤y<1, met fpart(x), die laat alleen de decimalen zien van x. vb: fpart(9.6)=0.6 en fpart(-9.6)=-0.6.
dus y=fpart(((11^3+(int(x)^3))^(1/3). Ik kom uit op een domein van 1≤x≤21 (juist?). met calc:zero zou deze functie voor x geen oplossing bieden. In table zie je dan met ∆tbl=1, geen 0 voor y, maar table doorlopen is kan meer werk zijn.
dus y=fpart(((11^3+(int(x)^3))^(1/3). Ik kom uit op een domein van 1≤x≤21 (juist?). met calc:zero zou deze functie voor x geen oplossing bieden. In table zie je dan met ∆tbl=1, geen 0 voor y, maar table doorlopen is kan meer werk zijn.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
-
magicsander
- Vast lid

- Berichten: 58
- Lid geworden op: 09 jul 2009, 19:01
Re: de stelling van Fermat (voor een bepaalde set getallen)
Owjaah xD,
Derdemachten........
dan moet het dus zijn:
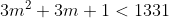
^^ derdemachten maken de boel alleen maar makkelijker
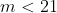
Derdemachten........
dan moet het dus zijn:
^^ derdemachten maken de boel alleen maar makkelijker
Re: de stelling van Fermat (voor een bepaalde set getallen)
Hmm allesinds geen negertjes. Ik ga nu het verhaal niet vertellen anders heb je er ook niet veel meer aanMathematica schreef:nice...
is dat niet zo een film die qua verhaal een beetje lijkt op 'tien kleine negertjes' van Agatha Christie?
een groep mensen die is opgesloten samen met een moordenaar, en dan uiteindelijk elkaar allemaal vermoorden omdat ze elkaar ervan verdenken de moordenaar te zijn, of zoiets... ik weet het niet exact, maar ik geloof dat het zoiets was...
Ik zou die wel eens willen zien
een andere leuke film met wiskunde in is 'The Oxford Murders'...
-
Mathematica
- Vast lid

- Berichten: 41
- Lid geworden op: 29 nov 2009, 12:26
Re: de stelling van Fermat (voor een bepaalde set getallen)
ja, dat is wel waar... 
life is physics, love is chemistry, everything is mathematics...

