bewijs (misschien). Kan jij dit vinden?
bewijs (misschien). Kan jij dit vinden?
Ik zie de prof. vrijdagmiddag om 16.00. Daarna volgt een treinreis, dus als alles lukt, staat het vrijdagavond online als een raadsel in dit topic.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: bewijs (misschien)
Dit kan ik wel alvast zelf bewijzen 
Ik presenteer het als een puzzel,
Dit is een mooie oefening voor recursieve formules.
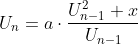 met 0<a<1 en m,x>0 (m<0 heeft een andere oplossing)
met 0<a<1 en m,x>0 (m<0 heeft een andere oplossing)
Naarmate n groter wordt, naar welke waarde convergeert deze rij?
Veel plezier!
Ik presenteer het als een puzzel,
Dit is een mooie oefening voor recursieve formules.
Naarmate n groter wordt, naar welke waarde convergeert deze rij?
Veel plezier!
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: bewijs (misschien)
Ik ben bij de prof. geweest. Hij wist niet hoe dit te bewijzen, maar kon het ook niet weerleggen. Hij heeft me aangeraden te leren programmeren, om evt. mocht het onjuist zijn, tegenvoorbeelden te zoeken, en boeken te lezen over rijen en reeksen, in de hoop dat daar een methode wordt aangeboden om dergelijk bewijs te vinden. Ik post ook dit als een puzzel.
gegeven:
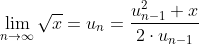 met
met 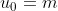 en
en 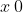 .
.
Bereken . Valt er iets op?
. Valt er iets op?
gegeven:
Bereken
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: bewijs (misschien)
Als je n naar oneindig laat gaan en aanneemt dat u[n] convergeert, betekent dit dat uiteindelijk u[n]=u[n-1], dus
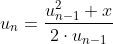
verandert in
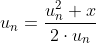
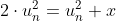
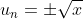
Nu moet je alleen nog bekijken voor welke u[0] bovenstaande convergeert.
In je eerdere post stel je al dat je de algemenere formule (voor 0 < a < 1) kan bewijzen, maar dan moet a=0.5 toch ook lukken? Klopt dit probleem wel?
verandert in
Nu moet je alleen nog bekijken voor welke u[0] bovenstaande convergeert.
In je eerdere post stel je al dat je de algemenere formule (voor 0 < a < 1) kan bewijzen, maar dan moet a=0.5 toch ook lukken? Klopt dit probleem wel?
Re: bewijs (misschien). Kan jij dit vinden?
Duidelijk is dan
We maken voor het gemak een nieuwe rij:
Schrijf
Dan gaat de recursie over is
We tonen aan dat
Stel
dan is
De rij
Stel die limiet is
Neem in de vergelijking (*) links en rechts de limiet. Resultaat:
Blijkbaar is
Stel
Re: bewijs (misschien). Kan jij dit vinden?
Er is al eerder in dit forum geschreven over de benadering voor 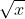 met de recursieve formule, en die bleek te kloppen. Het maakt niet uit welke reële waarde je voor
met de recursieve formule, en die bleek te kloppen. Het maakt niet uit welke reële waarde je voor 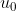 kiest. Die staat meer hier uitgelegd.
kiest. Die staat meer hier uitgelegd.
Wat op=op schreef, klopt, hoewel de redenatie me hier en daar wat ver gaat. de rij convergeert naar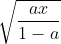 . Dat raadseltje is dus opgelost, maar waar ik naartoe wil is de uitdrukking van
. Dat raadseltje is dus opgelost, maar waar ik naartoe wil is de uitdrukking van
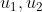 etc. in m en x voor a=0.5.
etc. in m en x voor a=0.5.
Ik zal een aantal geven.
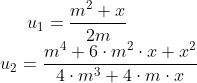
In de coëfficiënten lijkt me een regelmaat te zitten. Ik vraag me af of jullie die ook kunnen vinden.
edit: ik had dit als bewijsje voor de convergentie. Klopt dit?
als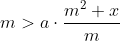
dan)
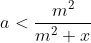
Het laatste blijkt te gelden, want 0<a<1.
Wat op=op schreef, klopt, hoewel de redenatie me hier en daar wat ver gaat. de rij convergeert naar
Ik zal een aantal geven.
In de coëfficiënten lijkt me een regelmaat te zitten. Ik vraag me af of jullie die ook kunnen vinden.
edit: ik had dit als bewijsje voor de convergentie. Klopt dit?
als
dan
Het laatste blijkt te gelden, want 0<a<1.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: bewijs (misschien). Kan jij dit vinden?
Je "bewijsje" voor de convergentie klopt niet. In de link die je geeft staat niets uitgelegd.
Voor de n-de term van het rijtje grijp ik liever terug naar mijn rijtje v's die een factor schelen met het rijtje u's.
Er geldt:b_{n+1}}{v_0 + (v_0-1)b_n})
met
^{k+1}{{n-2j}\choose {k-2j}}a^{n-k})
Voor de n-de term van het rijtje grijp ik liever terug naar mijn rijtje v's die een factor schelen met het rijtje u's.
Er geldt:
met
Re: bewijs (misschien). Kan jij dit vinden?
Kan je me uitleggen wat er niet klopt aan het "bewijsje"? Ik doelde in de link naar formules; iteratief oplossen van de wortel. Daar wordt een voorbeeld gegeven. Ik was op zoek naar iets anders; met 
Over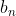 : Hier moet gelden dat 2j≤k en 2j≤n, als ik n=4, j=1, k=0 gebruik, kom ik uit op
: Hier moet gelden dat 2j≤k en 2j≤n, als ik n=4, j=1, k=0 gebruik, kom ik uit op
^1 {4-2 \choose 0-2} a^{4-0}=\\ -1\cdot {2 \choose -2}\cdot a^4)
Bedoelde je dat, of werkt je formule anders??
Over
Bedoelde je dat, of werkt je formule anders??
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: bewijs (misschien). Kan jij dit vinden?
Wat jij aantoont is dat 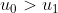 .
.
Dat lijkt me te weinig voor een bewijs.
In mijn formule moet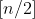 vervangen worden door
vervangen worden door 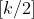 .
.
Dat lijkt me te weinig voor een bewijs.
In mijn formule moet
Re: bewijs (misschien). Kan jij dit vinden?
Ik ben uitgegaan van een generalisatie, ik zal het dan anders proberen.
als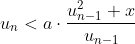
dan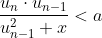
Lastig.. maar zoiets.
Ik zal dat in je formule wijzigen. Wel creatief; als k=1, geldt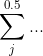
n=2
k=0:^1 {2 \choose 0}a^2)
k=1:^2 {2 \choose 1}a^1+(-1)^2 {1 \choose 0}a^1)
k=2:^3 {2 \choose 2}a^0+(-1)^3 {1 \choose 1}a^0+(-1)^3 {0 \choose 0}a^0)
als
dan
Lastig.. maar zoiets.
Ik zal dat in je formule wijzigen. Wel creatief; als k=1, geldt
n=2
k=0:
k=1:
k=2:
Laatst gewijzigd door David op 27 apr 2010, 13:49, 1 keer totaal gewijzigd.
Reden: toevoeging
Reden: toevoeging
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: bewijs (misschien). Kan jij dit vinden?
Je probeert vermoed ik te bewijzen dat de rij stijgend is.
Nou dat is ie soms wel en soms niet. Dat hangt van de waarde van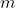 af. Dat is nog een heel gedoe.
af. Dat is nog een heel gedoe.
Met de rechte haken in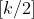 wordt een afronding naar het grootste gehele getal kleiner dan k/2 bedoeld (De floor in computertaal; de entier in wiskundetaal (spreek je uit op z'n Frans)).
wordt een afronding naar het grootste gehele getal kleiner dan k/2 bedoeld (De floor in computertaal; de entier in wiskundetaal (spreek je uit op z'n Frans)).
Nou dat is ie soms wel en soms niet. Dat hangt van de waarde van
Met de rechte haken in
Re: bewijs (misschien). Kan jij dit vinden?
Ok, dat wist ik niet, maar als ik naar LateX formules kijk, kan je floor weergeven als 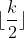
Ik probeer iets anders te bewijzen dan dat je voorstelt; kijk eens naar de coëfficienten van de getallen bij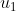 en
en 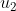 . Valt je iets op?
. Valt je iets op?
Ik probeer iets anders te bewijzen dan dat je voorstelt; kijk eens naar de coëfficienten van de getallen bij
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: bewijs (misschien). Kan jij dit vinden?
De floor wordt inderdaad vaak zo weergegeven.
De entier schrijf je in de wiskunde met rechte haken.
De entier schrijf je in de wiskunde met rechte haken.
Re: bewijs (misschien). Kan jij dit vinden?
Ok, wel wonderlijk dat ze voor twee dezelfde functies een andere notatie hebben, hoewel dit met vermenigvuldigen (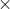 en
en  ) bijv. ook voorkomt.
) bijv. ook voorkomt.
Maar het raadsel blijft onopgelost.
Maar het raadsel blijft onopgelost.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
-
magicsander
- Vast lid

- Berichten: 58
- Lid geworden op: 09 jul 2009, 19:01
Re: bewijs (misschien). Kan jij dit vinden?
Ik ben niet goed met rekenregels voor sommaties, ik kan wel een programma schrijven om iets uit te testen voor een aantal waarden. Dus wat moet ik dan uittesten?


