Relatief priem
Relatief priem
Zij m en n natuurlijke getallen die relatief priem zijn, en a en b gehele getallen:
Bewijs dat:
1°als:
a=b (mod m) en a=b (mod n)
dan:
a=b (mod m.n)
2°Geldt dit ook als ggd(m,n) > 1?
1°vb: m=3, n=4
ggd(m,n) = 1 (dus relatief priem)
50 = 2 (mod 3) en 50 = 2 (mod 4)
=>50 = 2 (mod 3.4), dus geldig
2°vb: m=4, n=8
ggd(m,n) > 1 (dus niet relatief priem)
50 = 2 (mod 4) en 50 = 2 (mod 8 )
=>50 = 18 (mod 4.8 ) , dus niet geldig
m | (a-b)
n | (a-b)
=> m*n | (a-b)(a-b)
Hoe kan ik nu aantonen dat m*n|(a-b) en enkel wanneer m en n relatief priem zijn?
Bewijs dat:
1°als:
a=b (mod m) en a=b (mod n)
dan:
a=b (mod m.n)
2°Geldt dit ook als ggd(m,n) > 1?
1°vb: m=3, n=4
ggd(m,n) = 1 (dus relatief priem)
50 = 2 (mod 3) en 50 = 2 (mod 4)
=>50 = 2 (mod 3.4), dus geldig
2°vb: m=4, n=8
ggd(m,n) > 1 (dus niet relatief priem)
50 = 2 (mod 4) en 50 = 2 (mod 8 )
=>50 = 18 (mod 4.8 ) , dus niet geldig
m | (a-b)
n | (a-b)
=> m*n | (a-b)(a-b)
Hoe kan ik nu aantonen dat m*n|(a-b) en enkel wanneer m en n relatief priem zijn?
Laatst gewijzigd door vwpolo02 op 02 mei 2011, 23:40, 1 keer totaal gewijzigd.
Re: Relatief priem
Niemand die mij enige hint kan geven?
-
Sjoerd Job
- Vergevorderde

- Berichten: 1144
- Lid geworden op: 21 jan 2006, 15:09
- Locatie: Krimpen aan den IJssel
Re: Relatief priem
Wat je eigenlijk zou moeten bewijzen is: Als  = 1) en
en 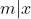 en
en 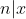 dan
dan 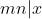 . (en dan dit toepassen op
. (en dan dit toepassen op 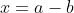 .). Ik ken uit mijn hoofd niet een bewijs hiervoor, maar weet wel dat het waar is. Welke voorkennis heb je?
.). Ik ken uit mijn hoofd niet een bewijs hiervoor, maar weet wel dat het waar is. Welke voorkennis heb je?
``Life is complex. It has real and imaginary parts.''
Re: Relatief priem
Is vraag voor een cursus discrete wiskunde. Ik zal mij hier al mee proberen te behelpen...
-
Sjoerd Job
- Vergevorderde

- Berichten: 1144
- Lid geworden op: 21 jan 2006, 15:09
- Locatie: Krimpen aan den IJssel
Re: Relatief priem
Gebruik bijvoorbeeld 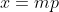 en
en 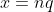 , dus
, dus  . Zie dit te gebruiken om bij
. Zie dit te gebruiken om bij ) te komen.
te komen.
``Life is complex. It has real and imaginary parts.''
Re: Relatief priem
Geraak er maar niet aan uit... Het feit dat elk getal een unieke priemontbinding heeft lijkt me hier wel van belang...
Re: Relatief priem
Kun je niet gebruiken dat als ggd(m,n)=1, de priemontbinding van m en n geen gelijke priemgetallen bevat. Omdat m|x en n|x zijn de priemontbindingen van m en n wel beide een gedeelte van de priemontbinding van x en dus die van mn ook en dus is mn|x.
Het is wat krom opgeschreven, maar ik heb het idee dat het wel klopt.
Het is wat krom opgeschreven, maar ik heb het idee dat het wel klopt.
Re: Relatief priem
Maar hoe toon je aan dat het niet zo is wanneer ze niet relatief priem zijn zoals in het 2e voorbeeld? Als je 2 getallen vermenigvuldigt die relatief priem zijn heb je hun kgv. In dit geval is dat dus a (+ b als rest)
-
Sjoerd Job
- Vergevorderde

- Berichten: 1144
- Lid geworden op: 21 jan 2006, 15:09
- Locatie: Krimpen aan den IJssel
Re: Relatief priem
Als ze niet relatief priem zijn, kan het nog wel waar zijn. Bijvoorbeeld:vwpolo02 schreef:Maar hoe toon je aan dat het niet zo is wanneer ze niet relatief priem zijn zoals in het 2e voorbeeld? Als je 2 getallen vermenigvuldigt die relatief priem zijn heb je hun kgv. In dit geval is dat dus a (+ b als rest)
Dat het niet altijd waar hoeft te zijn kan met een tegenvoorbeeld. (die heb je al gegeven).
Wat je kan gebruiken is dat omdat
``Life is complex. It has real and imaginary parts.''

