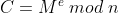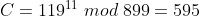webtest schreef: (vrij vertaald):
We hebben
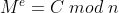
en specifiek
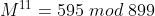
Is hieruit het getal M te vinden? Dus is deze formule om te draaien zodat je weer M = 119 krijgt?
Of is dit onmogelijk?
Voor kleine waarden van n is M terug te vinden, voor grote waarden van n niet.
Dat wil zeggen: voor kleine waarden lukt dit met de hand, voor grote waarden zelfs niet met de computer.
Hier is het RSA encryptiesysteem op gebaseerd.
[1] Kleine waarden van n:
- mogelijkheid 1: In de link van arno gaan ze alle restklassen af (0 t/m 898), dat is voor kleine getallen goed te doen.
- mogelijkheid 2:
a) ontbind 899 in factoren: 899 = 29*31 (snel)
b) eulerphi(899) = eulerphi(29*31) = (29-1)*(31-1) = 840 (supersnel)
c) bepaal de inverse van 11 mod 840: 611 (snel via het uitgebreide algoritme van Euclides)
d) bepaal M = 595^611 mod 899 = 119 mod 899 (snel via modulair machtsverheffen)
[2] Middelgrote n: bijvoorbeeld n = 225814191023 (een getal van 12 cijfers)
Voorbeeld: M^123456789101 = 153613986672 mod 225814191023
- mogelijkheid 1: Alle restklassen afgaan met een computer zal nu al erg lang gaan duren.
- mogelijkheid 2:
a) Ontbinden in factoren (2 factoren van 6 cijfers) is met computer nog redelijk snel te doen.
b) c) d): nog steeds snel.
Dus met mogelijkheid 2 is M nog terug te vinden.
[3] Grote n: bijvoorbeeld een getal van 100 cijfers:
nu gaat ook ontbinding in factoren (methode 2) te lang duren.
Dus zolang niemand hele grote getallen zeer snel kan ontbinden is het RSA systeem veilig.