---
Beste wiskundigen,
Ik heb mij hier aangemeld omdat ik met een meetkundige case zit waar ik zelf niet uit kom. Ik ben nooit heel handig in wiskunde geweest en ik hoop dat jullie mij kunnen helpen!
Het gaat om een praktijkprobleem uit een kleinschalig bedrijfje dat vloeren maakt. Deze vloeren bestaan uit 2 materialen: piepschuim en een speciaal mengsel dat varieert en verhard (hierna mix). Deze vloeren zijn meestal vierhoekig, maar hebben soms één schuine zijde. Met de volgende afbeelding zal ik een overdreven geval laten zien hiervan (verhoudingen kloppen overigens niet!):
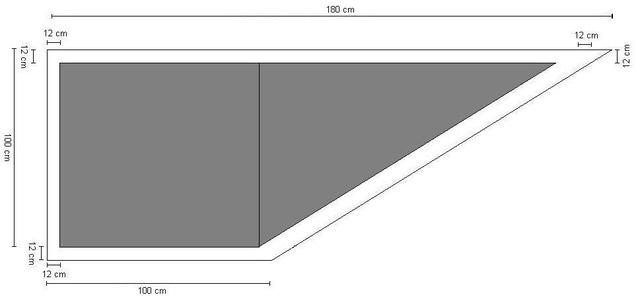
Het piepschuim (in het midden) moet altijd precies 12cm mix om zich heen krijgen (dus ook tussen de schuine zijde binnen en buiten). De maten van de buitenkant zijn bekend. Dat wil zeggen, de schuine zijde reken ik altijd met de stelling van pythagoras uit en dit is verder duidelijk. Het lukt mij echter niet om de juiste maten voor het piepschuim te vinden. Normaal benader ik dit altijd door standaard 12cm aan alle zijkanten eraf te halen (dus de lange zijde van in het voorbeeld 180cm wordt 180-24=156cm), de verticale wordt 100-24=76cm, etc. Dit klopt echter niet bij de schuine zijde. Deze komt op die manier namelijk minder dan 12cm van de rand te zitten. Ik heb wel wat theorieën hoe dit kan (ik reken rechtsboven bijv. vanaf de hoek, maar omdat het schuif afloopt wordt de afstand 12cm lager al kleiner), maar wat voornamelijk van belang is voor mij is hoe ik op correcte wijze - ook bij varianten met andere hoeken - gemakkelijk alle lengtes van het piepschuim kan vinden. Het liefst zou ik dit ook in excel willen kunnen berekenen door de maten van de buitenste vorm in te voeren. Ik heb zelf al met gelijkvormigheid zitten puzzelen maar mijn wiskundige kennis is simpelweg niet groot genoeg om er zelf uit te komen. De 12 cm geldt overigens altijd, hoe groot het vloertje ook wordt, in verband met de stevigheid.
Jullie zouden me geweldig helpen met een oplossing!


 Dank.U 12cm verschuiven van de horizontale en verticale lijn
Dank.U 12cm verschuiven van de horizontale en verticale lijn
