Het sigma-teken is hier de som voor k = 0 t/m oneindig van alle termen achter dit teken.
Je berekent eerst voor k=0 de term achter het sigma-teken, dan voor k=1, dan voor k=2, etc.
Doordat de termen snel kleiner worden hoef je gelukkig niet door te gaan tot oneindig, maar kan je al eerder stoppen. De snelheid waarmee de termen naar nul naderen wordt de convergentiesnelheid genoemd (dit bekijken ze voor verschillende reeksen op de wikipedia pagina die je noemt).
Een goede benaderingsformule heeft een snelle convergentie: je hoeft dan weinig termen te berekenen voor de nauwkeurigheid die je wenst.
Nu de uitwerking voor deze formule:
k=0:
 = \frac{1}{16^0}*\left(\frac{4}{8*0+1} - \frac{2}{8*0+4} - \frac{1}{8*0+5} - \frac{1}{8*0+6}\right) \approx 3.13333333)
k=1:
 = \frac{1}{16^1}*\left(\frac{4}{8*1+1} - \frac{2}{8*1+4} - \frac{1}{8*1+5} - \frac{1}{8*1+6}\right) \approx 0.00808913)
term(0) + term(1) ~= 3.13333333 + 0.00808913 = 3.14142247
k=2:
 = \frac{1}{16^2}*\left(\frac{4}{8*2+1} - \frac{2}{8*2+4} - \frac{1}{8*2+5} - \frac{1}{8*2+6}\right) \approx 0.00016492)
term(0) + term(1) + term(2) ~= 3.13333333 + 0.00808913 + 0.00016492 = 3.14158739
enzovoorts.
Hieronder zie je wat waarden voor k, term(k) en de som van term(0) t/m term(k):
Code: Selecteer alles
0 3.13333333 3.13333333
1 0.00808913 3.14142247
2 0.00016492 3.14158739
3 0.00000507 3.14159246
4 0.00000019 3.14159265
5 0.00000001 3.14159265
6 0.00000000 3.14159265
Je ziet dat je hier al behoorlijk snel een goede benadering voor pi krijgt.
Is dit wat je zoekt??
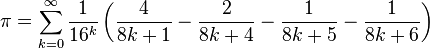 ) maar dat lukt mij niet
) maar dat lukt mij niet