Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Integraalrekening, afgeleiden, rijen, convergentie & divergentie van reeksen, meervoudige integratie.
-
Aniek
- Vergevorderde

- Berichten: 220
- Lid geworden op: 06 mar 2009, 12:49
Bericht
door Aniek » 06 sep 2009, 12:54
met welke formule bereken je deze integraal juis, ik mijn boek zegt alleen dat de rekenregels analoog zijn voor aan die voor afgeleiden, maar ik kom toch iets verkeerd uit.
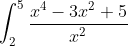
en als f(x)=tan^2x is F(x)dan F(x)=1/cos^4x???
nogmaals dank voor jullie hulp...

“Heal the world.” Michael Jackson
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 06 sep 2009, 13:15
Aniek schreef:met welke formule bereken je deze integraal juis, ik mijn boek zegt alleen dat de rekenregels analoog zijn voor aan die voor afgeleiden, maar ik kom toch iets verkeerd uit.
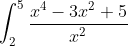
Werk eerst de deling
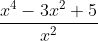
uit, en integreer dit resultaat door gebruik te maken van de formule voor de primitieve van
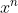
.
Aniek schreef:en als f(x)=tan^2x is F(x)dan F(x)=1/cos^4x???
nogmaals dank voor jullie hulp...

Maak gebruik van het gegeven dat tan x de afgeleide tan²x+1 heeft.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Aniek
- Vergevorderde

- Berichten: 220
- Lid geworden op: 06 mar 2009, 12:49
Bericht
door Aniek » 06 sep 2009, 15:33
ok, de eerst heb ik, de 2de nog niet
tanx'=1/cos²x, hoe kom je aan tan²x+1?
bedankt
“Heal the world.” Michael Jackson
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 06 sep 2009, 20:08
Ga uit van sin²x+cos²x=1 en gebruik dit om de teller in
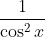
uit te werken.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Aniek
- Vergevorderde

- Berichten: 220
- Lid geworden op: 06 mar 2009, 12:49
Bericht
door Aniek » 07 sep 2009, 09:19
zo dan:
f'(x)=tan²x=>F(x)=(1/cos²x)²=sin²xcos²x/cos^4(x)=tan²x+1
dank je wel
“Heal the world.” Michael Jackson
-
arie
- Moderator

- Berichten: 3917
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 08 sep 2009, 11:18
Probeer alles stap voor stap te doen:
[1] Eerst herschrijf je de afgeleide van tan(x):
Je weet al:
 = \frac{1}{cos^2(x)})
en
 + cos^2(x) = 1)
Dus, zoals arno hierboven heeft beschreven:
 = \frac{1}{cos^2(x)} = = \frac{sin^2(x) + cos^2(x)}{cos^2(x)} = tan^2(x)+1) [2] Vervolgens bepaal je de primitieve van tan^2(x):
[2] Vervolgens bepaal je de primitieve van tan^2(x):
Je zoekt een functie, zeg f(x), waarvoor f '(x) = tan^2(x).
Hierboven heb je gevonden dat tan'(x) = tan^2(x)+1
Gebruik dit om een functie g(x) vinden zodat:
 = tan(x) + g(x))
en zodat (via de somregel, zie bijv. punt 4 op
http://nl.wikibooks.org/wiki/Analyse/Differentiatie):
 = tan'(x) + g'(x) = (tan^2(x)+1) + g'(x) = tan^2(x))
Als je g(x) hebt, dan heb je ook f(x) en weet je ook een primitieve van tan^2(x).
Lukt het zo?
-
Aniek
- Vergevorderde

- Berichten: 220
- Lid geworden op: 06 mar 2009, 12:49
Bericht
door Aniek » 14 sep 2009, 15:30
oh, ik had niet gezien dat je hier nog op had geantwoord, nu is het duidelijk ja... dankjewel

g(x)=-x
“Heal the world.” Michael Jackson

