Voor toepassingen van SVD zie:
http://en.wikipedia.org/wiki/Singular_v ... omposition
De toepassing als kleinste kwadraten oplosser is het meest vor de hand liggend om te vermelden.
LU-decompositie kan gebruikt worden om een oplossing van een stelsel vergelijkingen te vinden met evenveel verelijkingen als onbekenden.
Als voor een stelsel vergelijkingen het aantal rijen ongelijk is aan het aantal onbekenden, dan kun je naar een kleinste kwadraten oplossing zoeken met SVD.
Vraag 1:
Als
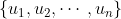
een basis is van eigenvectoren, dan is de matrix van L een diagonaalmatrix.
Want als
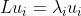
voor
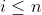
, dan is
 = \mbox{ diag}(\lambda_1, \lambda_2,\cdots,\lambda_n)(u_1 u_2 \cdots u_n))
Hier is
)
de nxn matrix met de eigenvectoren als kolommen.
en hieruit volgt
^{-1}L(u_1 u_2 \cdots u_n) = \mbox{ diag}(\lambda_1, \lambda_2,\cdots,\lambda_n))
.
Vraag 2:

(directe som).
Dat betekent dat elke
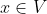
te schrijven is als
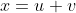
met
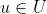
en
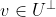
.
Als
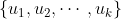
een basis is van onafhankelijke vectoren van
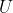
en
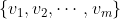
een basis is van onafhankelijke vectoren van
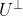
,
dan is zeg
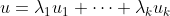
en
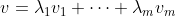
en dus

.
Als we kunnen aantonen dat alle
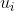
's en
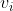
's onafhankelijk zijn,
dan hebben we aangetoont dat elke
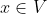
te schrijven is als een lineaire combinatie van m+k onafhankelijke vectoren. Die m+k vectoren zijn dan per definitie een basis van
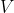
.
en dus geldt dim(U) + dim(U(loodrecht)) = dim(V).
De
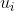
's en
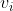
's zijn onafhankelijke vectoren.
Elke
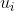
is onafhankelijk van de verzameling vectoren
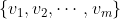
,
want als

,
en
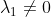
, dan is
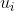
uit te drukken in een lineaire combinatie van
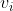
's. Maar dat kan niet want
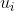
zit niet in
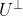
omdat
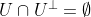
Analoog is elke
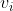
is onafhankelijk van de verzameling vectoren
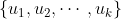
.
Vraag 3: Het Gram Schmidt orthogonalisatie proces.
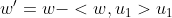
Merk op dat
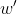
loodrecht staat op
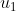
,
want neem maar het inprodukt met
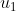
:
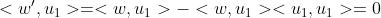
.
De
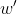
wordt daarna genormaliseerd en
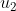
genoemd.


