Pagina 1 van 1
Reele Vectorruimten
Geplaatst: 23 apr 2011, 18:02
door Kinu
Het is al weer een heel tijdje geleden dat ik Reele Vectorruimten heb gezien en ik was het terug wat aan het opfrissen. Ik probeerde daarom enkele (''gemakkelijke'') oefeningen.
Gevraagd:
Zij de vector p een lineaire combinatie van de vectoren
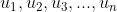
en als elk van de vectoren
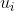
een lineaire combinatie is van de vectoren
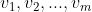
dan is de vector p een lineaire combinatie van de vectoren
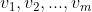
. Bewijs dit.
Omdat de vector
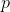
een lineaire combinatie is van de gegeven vectoren
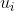
geldt er:
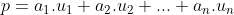
En:
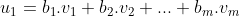
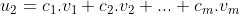
...
Dus ik kan schrijven:
+a_2.(c_1.v_1+c_2.v_2+...+c_m.v_m)+...+a_n(q_1.v_1+q_2.v_2+...q_m.v_m))
Maar heb ik hiermee dan de stelling bewezen?
Re: Reele Vectorruimten
Geplaatst: 24 apr 2011, 13:56
door Huibert
Om het nog duidelijker te maken, zou je die laatste stap nog uit kunnen schrijven. Maar bewezen is het zo wel, je hebt namelijk gewoonweg die willekeurige vector als lineaire combinatie geschreven. Dat dat kon, moest je bewijzen.
Re: Reele Vectorruimten
Geplaatst: 24 apr 2011, 14:29
door Kinu
Huibert schreef:Om het nog duidelijker te maken, zou je die laatste stap nog uit kunnen schrijven. Maar bewezen is het zo wel, je hebt namelijk gewoonweg die willekeurige vector als lineaire combinatie geschreven. Dat dat kon, moest je bewijzen.
Ok! Bedankt voor je reactie

.
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 00:43
door Kinu
Ik kwam de notatie
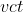
tegen. Wat betekent dit eigenlijk?
Opgave:
Als
)
een basis is van
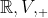
en als
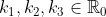
dan is ook
)
een basis van
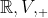
Toon dit aan.
Opdat de vectoren
)
een basis vormen moeten ze lineair onafhankelijk zijn en wil dat zeggen dat ik er geen enkele van als een lineaire combinatie van de overige kan schrijven en bovendien moet elke vector van die basis kunnen geschreven worden als een lineaire combinatie van die drie basisvectoren kan geschreven worden.
Stel
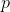
is een vector die tot de basis
)
behoort dan moet er voor p gelden:
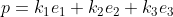
Bijgevolg is dus
)
ook een basis.
Graag commentaar.
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 01:12
door Huibert
De notatie vct ken ik niet. In welke context stond dit? En betekent dit niet gewoon vector?
Ook je notatie voor de vectorruimte snap ik niet helemaal. Ik denk dat je het hebt over een willekeurige vectorruimte V over
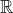
, maar wat bedoel je met het +-teken?
Ik denk wel dat ik de opgave goed begrijp. Maar je hebt het op deze manier nog niet helemaal aangetoond. Wat je hebt aangetoond, is dat elke vector uit de vectorruimte als een lineaire combinatie van deze drie vectoren te schrijven is. Je hebt nog niet aangetoond dat ze lineair onafhankelijk zijn. Dit is redelijk simpel, maar als je het goed wil doen, moet je dat wel even aantonen.
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 01:35
door Kinu
Huibert schreef:De notatie vct ken ik niet. In welke context stond dit? En betekent dit niet gewoon vector?
Ook je notatie voor de vectorruimte snap ik niet helemaal. Ik denk dat je het hebt over een willekeurige vectorruimte V over
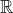
, maar wat bedoel je met het +-teken?
Ik denk wel dat ik de opgave goed begrijp. Maar je hebt het op deze manier nog niet helemaal aangetoond. Wat je hebt aangetoond, is dat elke vector uit de vectorruimte als een lineaire combinatie van deze drie vectoren te schrijven is. Je hebt nog niet aangetoond dat ze lineair onafhankelijk zijn. Dit is redelijk simpel, maar als je het goed wil doen, moet je dat wel even aantonen.
Deze notatie 'vct' kwam ik tegen in een nogal redelijk oud boek, het zou kunnen dat het gewoon vector betekent.
Dat + teken staat ervoor dat de optelling is gedefinieerd in een reele vectorruimte. Ik heb deze notatie altijd zo aangeleerd. Hoe zou jij het dan schrijven?
Aantonen dat de vectoren lineair onafhankelijk zijn, ik dacht aan een beroep te doen op een stelling:
Als
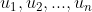
vectoren zijn van een reele Vectorruimte en bovendien
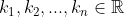
dan geldt er dat:
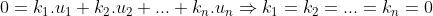
[/tex]
Stel dus dat de vector p de nulvector is en we weten dat de vectoren
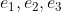
lineair onafhankelijk zij dan geldt er:
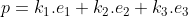
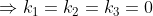
Ingevuld zou dat moeten zeggen dat
)
een basis is maar dat kan niet want dan zouden de vectoren lineair afhankelijk moeten zijn dus bijgevolg zijn de vectoren lineair onafhankelijk.
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 02:12
door Huibert
Ik heb geleerd dat er op een vectorruimte per definitie een optelling gedefinieerd is.
Ik zal hieronder een volledig bewijs geven van de stelling (en dan in een iets algemenere zin, want ik zie niet in waarom er beperkt wordt tot reële vectorruimten), want ik zag dat ik nog iets in je vorige bewijs over het hoofd heb gezien.
Stelling:
Als V een vectorruimte is over
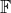
en
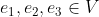
vormen een basis van V, dan vormen

met
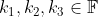
een basis van V.
Bewijs:
Zij

. Dan is v te schrijven als:
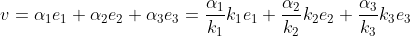
met:
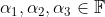
Stel nu dat:
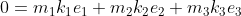
met:
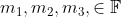
dan volgt per definitie dat:
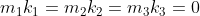
en dus:
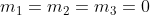
Dit omdat de k's niet nul mogen zijn (dan zou je een nulvector in je basis krijgen en heb je dus geen basis meer)
Hiermee volgt dat elke vector v uit V te schrijven is als een lineaire combinatie van het stelsel

en dat dit stelsel lineair onafhankelijk is en hiermee volgt dus de stelling.
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 10:33
door Kinu
Mooi bewijs

, ik zie nu dat mijn bewijs wel in de goede richting zat, maar niet zo uitgewerkt en volledig is als dat van u.
Ik vind het leuk om zelf eigenschappen of stellingen proberen te bewijzen dus ik zal er zeker nog wel posten.
Al erg bedankt voor je hulp!
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 10:43
door Huibert
Het kan ook nog wel sneller. Als je aantoont dat die drie vectoren onafhankelijk zijn, ben je eigenlijk al klaar. Dit omdat als één basis in een vectorruimte uit drie vectoren bestaat, alle bases in die vectorruimte uit drie vectoren bestaan. Maar ik wist niet of je die stelling al gezien had.
En ik heb nog wel een leuke stelling voor je om te bewijzen:
Dim(Ker(T)) + Dim(Range(T)) = Dim(V)
Waarbij T een lineaire transformatie van V naar W.
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 10:59
door Kinu
Huibert schreef:Het kan ook nog wel sneller. Als je aantoont dat die drie vectoren onafhankelijk zijn, ben je eigenlijk al klaar. Dit omdat als één basis in een vectorruimte uit drie vectoren bestaat, alle bases in die vectorruimte uit drie vectoren bestaan. Maar ik wist niet of je die stelling al gezien had.
En ik heb nog wel een leuke stelling voor je om te bewijzen:
Dim(Ker(T)) + Dim(Range(T)) = Dim(V)
Waarbij T een lineaire transformatie van V naar W.
Het zou kunnen dat ik die stelling ooit gezien heb, maar dat weet ik niet meer goed. Voor je volgende vraag:
Ik zie er dimensie en kern van een vectorruimte in, maar het begrip 'kern en range' heb ik nog niet gezien, ik heb er wel al over gehoord. Misschien dat u er wat meer over kan vertellen. Ook lineaire transformaties, lineaire afbeeldingen, ... heb ik nog niet gezien.
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 17:09
door arno
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 21:26
door Huibert
Als je na het lezen van die wikipedia pagina nog vragen heb, stel je ze maar. Dit zijn trouwens allemaal dingen uit de lineaire algebra. Erg interessant allemaal, ook al heb ik er nog niet heel veel van gehad.
Re: Reele Vectorruimten
Geplaatst: 25 apr 2011, 21:28
door Kinu
Huibert schreef:Als je na het lezen van die wikipedia pagina nog vragen heb, stel je ze maar. Dit zijn trouwens allemaal dingen uit de lineaire algebra. Erg interessant allemaal, ook al heb ik er nog niet heel veel van gehad.
Ja, lineaire algebra vind ik opzich wel interessant, omdat het zo abstract is wat het nogal moeilijk maakt. Ik vind het in ieder geval moeilijker dan analyse. Maar ik zal er eens een kijkje naar nemen

.
Re: Reele Vectorruimten
Geplaatst: 21 jul 2011, 11:49
door Kinu
Ik weet nu wat de notatie 'vct' betekent, bijvoorbeeld als er zou staan:
)
, dit is de de verzameling van de lineaire combinaties van de vectoren

.
Huibert schreef:
Dim(Ker(T)) + Dim(Range(T)) = Dim(V)
Waarbij T een lineaire transformatie van V naar W.
Over dit bewijs ga ik nog eens nadenken, ik ben al bekend met de begrippen kern en dimensie e.d, maar ik moet er nog wat met leren werken

.
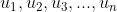 en als elk van de vectoren
en als elk van de vectoren 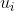 een lineaire combinatie is van de vectoren
een lineaire combinatie is van de vectoren 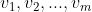 dan is de vector p een lineaire combinatie van de vectoren
dan is de vector p een lineaire combinatie van de vectoren 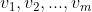 . Bewijs dit.
. Bewijs dit.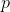 een lineaire combinatie is van de gegeven vectoren
een lineaire combinatie is van de gegeven vectoren 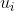 geldt er:
geldt er: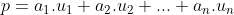
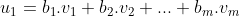
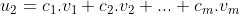
+a_2.(c_1.v_1+c_2.v_2+...+c_m.v_m)+...+a_n(q_1.v_1+q_2.v_2+...q_m.v_m))