Partieel differentiëren

[logicisthekey]

Ik heb veel onderwerpen gelezen, maar ik kom er nog steeds niet uit.
Partieel differentiëren snap ik wel! alleen als in de formule ''e'' voorkomt.. dan weet ik het niet.

Ofterwijl= g= 4x^2y

xg= 8xy < dit snap ik en de rest ook natuurlijk allemaal.

Maar nu:

Formule: f (x, y) = ye^xy

xf = y²e^xy

yf= e^xy + xye^xy

x²f= y³e^xy

y^2f= xe^xy + xe^xy + x²ye^xy
= 2xe^xy + x²ye^xy

Dit is de formule + gedeff. Ik snap totaal niet hoezo bij xf y^2 wordt en bij yf al helemaal niks.
Miss is er een bepaalde regel of iets dergelijks?

[SafeX]

Wat is de afgeleide (naar x) van:
1. e^x
2. e^(3x)

Is je functie:

Zo ja, waarom is dan de notatie f(x,y)=ye^xy fout?

[logicisthekey]

Is je functie:

Wat is de afgeleide (naar x) van:
1. e^x
2. e^(3x)

Dat weet ik dus niet, ik heb op internet gekeken, maar kom er niet uit. Andere opdrachten die ik gemaakt heb. Laten ze de e buiten beschouwing en deff. ze een ander gedeelte ervan.

Is je functie:

Zo ja, waarom is dan de notatie f(x,y)=ye^xy fout?

De formule die jij hebt aangegeven is indderdaad de formule. Ik noteerde het met ye^xy , dacht dat dat het handigste was.

[logicisthekey]

Ik heb wat te gehaast geanwoord.

Afgeleide van e^x is e^x

van e^(3x) neem ik aan 2e^3x, omdat e^x als je deff. e^x is.

[logicisthekey]

Misschien is mijn vraag ook onduidelijk: f (x, y) = ye^xy


xf = y²e^xy
Waarom als je de functie diff. komt de Y in de macht? (waarom is dat eerder geen x?)

yf= e^xy + xye^xy
Waarom als je de functie diff. komt er een x bij xye^xy en waarom e^xy?

[David]

hoi logicisthekey,

wat ik weet van differentieren van een functie f(x)=e^(ax), f'(x)=a*e^(ax). (a is afgeleide van ax). bewijs ken ik niet van die regel, maar het idee is dat f(x)=e^(2x)=e^x*e^x. en dan f'(x) met productregel. zoiets is dan dat bewijsje, maar hetzelfde kan je doen voor f(x)=e^(3x).

[SafeX]

Je vraag is niet onduidelijk. Wat wel duidelijk is: je kent de kettingregel niet of past deze niet toe.
De afgeleide (naar x) van e^(3x) is 3e^(3x).
Je neemt 'in gedachten' 3x=u, dan differentieer je eerst naar u (dus 3x) en dan, de kettingregel, differentieer je 3x naar x, dat geeft 3. Het resultaat is dan het product van e^(3x) en 3.

Zo moet je ook jouw functie differentiëren.
Maar staat er nu: f(x,y)=ye^(xy) of ye^xy, dat is nl niet hetzelfde (wat is het verschil). Zie ook m'n eerdere post.
Ik begrijp dat je eerst partieel differentieert naar x (dus y constant).
Nu jij ...

[logicisthekey]

Oke, bij dit soort functies moet je altijd de kettingregel toepassen dus.

Er staat : f(x,y)=ye^(xy) (dus x & y beide in de macht)

[logicisthekey]

oo ineens schiet het een beetje te binnen.

ye^(xy) moet natuurlijk (afgeleid naar x) : y²e^(xy) zijn.

Met de uitleg van daco '' f(x)=e^(ax), f'(x)=a*e^(ax)''

Ofterwijl Functie * y.

Ok nu snap ik het afleiden naar x.

Maar wat doen ze precies bij het afleiden naar y?

daar is het antwoord: yf= e^(xy) + xye^(xy)

Ik begrijp het deel xye^(xy) , dan is de ''a'' zoals daco zegt de x. Maar hoe komen ze aan e^(xy).

[arno]

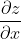
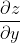
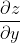
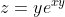
Stel z = f(x,y) is een functie van x en y, dan bepaal je door y als een constante te beschouwen, en bepaal je door x als een constante te beschouwen. Wat levert dit op voor als , en welke regels voor het differentiëren pas je hierbij toe?

[logicisthekey]

z= ye^(xy) Ik zou: f(x)=e^(ax), f'(x)=a*e^(ax)''

ofterwijl: xye^(xy) . diff.

[SafeX]

Bij afleiden naar y heb je ook te maken met de productregel.
Hoe differentieer je (naar x): f(x)=xe^(2x)

[logicisthekey]

Bij afleiden naar y heb je ook te maken met de productregel.
Hoe differentieer je (naar x): f(x)=xe^(2x)

Diff: 2e^(2x) (een of ander manier moet de e altijd dezelfde blijven)

Maar ik snap het al.

Bedankt voor de hulp allemaal!

[SafeX]

Bij afleiden naar y heb je ook te maken met de productregel.
Hoe differentieer je (naar x): f(x)=xe^(2x)

Diff: 2e^(2x) (een of ander manier moet de e altijd dezelfde blijven)

Maar ik snap het al.
Bedankt voor de hulp allemaal!

Diff: 2e^(2x) (een of ander manier moet de e altijd dezelfde blijven)

Maar ik snap het al.???

Maar dit is niet goed.