Onbepaalde integraal
Onbepaalde integraal
Kan iemand mij op weg helpen om deze integraal op te lossen?
Alvast bedankt
∫1/(SQRT(4-64(x)^2))dx
Alvast bedankt
∫1/(SQRT(4-64(x)^2))dx
Re: Onbepaalde integraal
Je bent er nog ...
Je zou (bv) eerst door 64 onder het wortelteken kunnen delen, waarom denk je?
Kan je een y= ... (met x) bedenken zodat je de wortel kwijt raakt?naomi schreef:∫1/(SQRT(4-64(x)^2))dx
Je zou (bv) eerst door 64 onder het wortelteken kunnen delen, waarom denk je?
Re: Onbepaalde integraal
Bedoel je bijvoorbeeld y=2 waardoor de som als volgt wordt?
∫1/(2-2^3))dx
∫1/(2-2^3))dx
Re: Onbepaalde integraal
4-
Stel nu: y=1/4cos(t), ga eens verder.
(4-64x²)/64=1/16-x²=(1/4)²-x²SafeX schreef:Je bent er nog ...Kan je een y= ... (met x) bedenken zodat je de wortel kwijt raakt?naomi schreef:∫1/(SQRT(4-64(x)^2))dx
Je zou (bv) eerst door 64 onder het wortelteken kunnen delen, waarom denk je?
Stel nu: y=1/4cos(t), ga eens verder.
Re: Onbepaalde integraal
Helaas kom ik er nog steeds niet uit. Ik begrijp hoe je aan 1/4^2-^x^2, maar weet niet hoe ik dit moet omzetten naar y=1/4cos(t)
Re: Onbepaalde integraal
Heeft deze integraal te maken met arcsin?
Re: Onbepaalde integraal
Ai, mijn fout, Het moet zijn x=1/4 cos(t).naomi schreef:Helaas kom ik er nog steeds niet uit. Ik begrijp hoe je aan 1/4^2-^x^2, maar weet niet hoe ik dit moet omzetten naar y=1/4cos(t)
Re: Onbepaalde integraal
∫1/(SQRT(4-64(x)^2))dx= ∫1/(1/16-x^2)= ∫1/(1/16-(1/4cos)^2)
Re: Onbepaalde integraal
Waar is sqrt gebleven???
sqrt(1/16-1/16cos²(t))=1/4sqrt(1-cos²(t))=...
sqrt(1/16-1/16cos²(t))=1/4sqrt(1-cos²(t))=...
Re: Onbepaalde integraal
1/4∫1/(1-cos^2(t))
Re: Onbepaalde integraal
Zet de zaken eens op een rijtje.
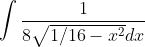
Stel x=1/4cos(t) => dx=...dt
}}...dt)
Wat wordt de wortel ... ?
Delen door 64 onder de wortel beteken een factor 8 voor de wortel.naomi schreef: ∫1/(SQRT(4-64(x)^2))dx
Stel x=1/4cos(t) => dx=...dt
Wat wordt de wortel ... ?
Re: Onbepaalde integraal
Het is mij niet helemaal duidelijk dat delen door 64 onder de wortel, betekent dat een factor 8 voor de wortel komt.
Re: Onbepaalde integraal
Werkt dit verhelderend?
Re: Onbepaalde integraal
ja het is helder.
Is deze formule cos2x=2(cos^2)x-1 van toepassing voor de wortel?
Is deze formule cos2x=2(cos^2)x-1 van toepassing voor de wortel?
Re: Onbepaalde integraal
Het is de bekende formule sin²(x)+cos²(x)=1 voor alle x. Dus: 1-cos²(x)=...
En zo raak je de wortel kwijt. Eens?
En zo raak je de wortel kwijt. Eens?

