wortels van breuken in standaardvorm
wortels van breuken in standaardvorm
Dag allemaal,
Ik ben momenteel bezig met het boek 'basisboek wiskunde' van Jan van de Craats. Echter loop ik ergens tegenaan waar vrijwel geen uitleg over wordt gegeven. De sommen waar ik tegenaan loop zijn als volgt:
(wortel2/3)3de macht
(2wortel3/3wortel2)3de macht
Ik kan niet goed doorgronden welke stappen ik moet zetten om deze sommen op te lossen.
Please help me out!
Groeten,
Sven
Ik ben momenteel bezig met het boek 'basisboek wiskunde' van Jan van de Craats. Echter loop ik ergens tegenaan waar vrijwel geen uitleg over wordt gegeven. De sommen waar ik tegenaan loop zijn als volgt:
(wortel2/3)3de macht
(2wortel3/3wortel2)3de macht
Ik kan niet goed doorgronden welke stappen ik moet zetten om deze sommen op te lossen.
Please help me out!
Groeten,
Sven
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: wortels van breuken in standaardvorm
Maak gebruik van de regel datsvenh1989 schreef:Dag allemaal,
Ik ben momenteel bezig met het boek 'basisboek wiskunde' van Jan van de Craats. Echter loop ik ergens tegenaan waar vrijwel geen uitleg over wordt gegeven. De sommen waar ik tegenaan loop zijn als volgt:
(wortel2/3)3de macht
(2wortel3/3wortel2)3de macht
Ik kan niet goed doorgronden welke stappen ik moet zetten om deze sommen op te lossen.
Please help me out!
Groeten,
Sven
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: wortels van breuken in standaardvorm
Als ik het volgens die methodiek probeer kom ik er nog steeds niet uit en ik geloof dat ik nog steeds ergens de mist in ga. Ik zal je laten zien hoe ik het uitwerk:
(wortel2/3)derde macht
Stap 1: wortel 2 tot de derde macht = 4
Stap 2: 3 tot de derde macht = 27
Antwoord: 4/27
Bij de tweede som loop ik helemaal in de knoop. Ik vroeg me af of je zou kunnen laten zien stap voor stap bij de tweede som hoe je het zou oplossen, en waar ik de mist in ga bij de eerste som.
Alvast bedankt voor de moeite!
(wortel2/3)derde macht
Stap 1: wortel 2 tot de derde macht = 4
Stap 2: 3 tot de derde macht = 27
Antwoord: 4/27
Bij de tweede som loop ik helemaal in de knoop. Ik vroeg me af of je zou kunnen laten zien stap voor stap bij de tweede som hoe je het zou oplossen, en waar ik de mist in ga bij de eerste som.
Alvast bedankt voor de moeite!
Re: wortels van breuken in standaardvorm
Is dit de opgave:
^3=...)
Eerst twee vragen:
1. wat betekent a^3 ...
2. Wat is:
^2=...)
Geef aan als je het antwoord op deze vragen niet weet!
Bewlangrijk: Het gebruik van de rekenregels (RR) zoals arno aangeeft moet je niet alleen weten maar ook begrijpen!
Eerst twee vragen:
1. wat betekent a^3 ...
2. Wat is:
Geef aan als je het antwoord op deze vragen niet weet!
Bewlangrijk: Het gebruik van de rekenregels (RR) zoals arno aangeeft moet je niet alleen weten maar ook begrijpen!
Re: wortels van breuken in standaardvorm
(wortela)2 interpreteer ik bijvoorbeeld als wortel 4 x wortel 4 = 4.
(wortela)3 interpreteer ik dan als bijvoorbeeld wortel 4 x wortel 4 x wortel 4 = 8
Het zou best kunnen dat ik dit fout interpreteer, ik vind het boek van Craats prettig werken, echter mis ik bij sommige onderdelen meer diepgang, oftewel waarom je iets doet en hoe de uitwerking eruit ziet.
Als je me kunt helpen om deze rekenregels beter te begrijpen, dan zou ik het zeer op prijs stellen.
(wortela)3 interpreteer ik dan als bijvoorbeeld wortel 4 x wortel 4 x wortel 4 = 8
Het zou best kunnen dat ik dit fout interpreteer, ik vind het boek van Craats prettig werken, echter mis ik bij sommige onderdelen meer diepgang, oftewel waarom je iets doet en hoe de uitwerking eruit ziet.
Als je me kunt helpen om deze rekenregels beter te begrijpen, dan zou ik het zeer op prijs stellen.
Re: wortels van breuken in standaardvorm
Dit klopt alleen als a=4svenh1989 schreef:(wortela)2 interpreteer ik bijvoorbeeld als wortel 4 x wortel 4 = 4.
(wortela)3 interpreteer ik dan als bijvoorbeeld wortel 4 x wortel 4 x wortel 4 = 8
Kan je ook mijn vragen beantwoorden:
Eerst twee vragen:
1. wat betekent a^3 ...
2. Wat is:
Geef aan als je het antwoord op deze vragen niet weet!
Re: wortels van breuken in standaardvorm
A^3 = AxAxA
(wortela)2 = Wortel a x Wortel a
Dat zou ik beantwoorden op de vragen vanuit mijn huidige kennis.
(wortela)2 = Wortel a x Wortel a
Dat zou ik beantwoorden op de vragen vanuit mijn huidige kennis.
Re: wortels van breuken in standaardvorm
Ok!
Echter:
(wortela)2 = Wortel a x Wortel a = a
^2=a)
Dat zou je moeten weten, want dat is de definitie van de vierkantswortel, ga dat na:
Je moet ook weten:
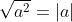
Wat is het verschil met de regel daarboven?
Nu jouw opgave: kan je het bovenstaande gebruiken?
Opm: gebruik voortaan de Latex-code.Je vind op dit forum dat als onderwerp.
Echter:
(wortela)2 = Wortel a x Wortel a = a
Dat zou je moeten weten, want dat is de definitie van de vierkantswortel, ga dat na:
Je moet ook weten:
Wat is het verschil met de regel daarboven?
Nu jouw opgave: kan je het bovenstaande gebruiken?
Opm: gebruik voortaan de Latex-code.Je vind op dit forum dat als onderwerp.
Re: wortels van breuken in standaardvorm
Ik begrijp de tweede formule niet, de eerste begrijp ik qua opbouw, maar wat het verschil is met de tweede zie ik niet.
Re: wortels van breuken in standaardvorm
svenh1989 schreef:Dag allemaal,
Ik ben momenteel bezig met het boek 'basisboek wiskunde' van Jan van de Craats. Echter loop ik ergens tegenaan waar vrijwel geen uitleg over wordt gegeven. De sommen waar ik tegenaan loop zijn als volgt:
(wortel2/3)3de macht
(2wortel3/3wortel2)3de macht
Ik kan niet goed doorgronden welke stappen ik moet zetten om deze sommen op te lossen.
Please help me out!
Groeten,
Sven
Ben je bekend met die rekenregels en kom je zo verder?
Nogmaals je som:
Re: wortels van breuken in standaardvorm
Heb je de definitie van de vierkantswortel nog eens bekeken?svenh1989 schreef:Ik begrijp de tweede formule niet, de eerste begrijp ik qua opbouw, maar wat het verschil is met de tweede zie ik niet.
Kies bij de tweede formule bv a=-2 ...
Hoe zit het nu met je opgave?

