De slak op het elastiek
De slak op het elastiek
Goedenavond,
Ik weet niet of dat hier mag , maar ik heb nog een vreemde vraag cq puzzel.
Dit gaat over een slak aan elastiek, ook hier zal het dan wel weer via een programmaatje op internet op te lossen zijn of is dit niet mogelijk.
Het volgende dus:
Stel je voor: een touw van 1 meter lang. En niet zo maar een touw, nee: het bijzondere aan dit touw is dat het van elastiek is gemaakt dat je oneindig kunt uitrekken, zonder dat het breekt. De uiteinden van dit touw noemen we A en B. Het touw is bij A vastgemaakt. Tevens bevindt zich bij uiteinde A, hoe verrassend: een slak.
Op een dag, laten we het dag 1 noemen, gebeurt er het volgende: de slak kruipt 5 cm richting B. Gelijk hierna wordt er bij B aan het touw getrokken, zodat het touw 1 meter langer wordt.
De volgende dag gebeurt er precies hetzelfde: de slak kruipt 5 cm richting B, en er wordt opnieuw bij B getrokken, zodat het touw weer een meter langer wordt. Het touw is na dag 2 dus al 3 meter lang.
De volgende dag... affijn, het patroon is duidelijk. De hamvraag: bereikt de slak ooit B? Het verrassende antwoord is ja! Maar op welke dag?
Je hoeft geen rekening te houden met fysieke beperkingen of randvoorwaarden zoals de kromming van de aarde en dergelijke. De puzzel is puur wiskundig van aard.
Ik weet niet of dat hier mag , maar ik heb nog een vreemde vraag cq puzzel.
Dit gaat over een slak aan elastiek, ook hier zal het dan wel weer via een programmaatje op internet op te lossen zijn of is dit niet mogelijk.
Het volgende dus:
Stel je voor: een touw van 1 meter lang. En niet zo maar een touw, nee: het bijzondere aan dit touw is dat het van elastiek is gemaakt dat je oneindig kunt uitrekken, zonder dat het breekt. De uiteinden van dit touw noemen we A en B. Het touw is bij A vastgemaakt. Tevens bevindt zich bij uiteinde A, hoe verrassend: een slak.
Op een dag, laten we het dag 1 noemen, gebeurt er het volgende: de slak kruipt 5 cm richting B. Gelijk hierna wordt er bij B aan het touw getrokken, zodat het touw 1 meter langer wordt.
De volgende dag gebeurt er precies hetzelfde: de slak kruipt 5 cm richting B, en er wordt opnieuw bij B getrokken, zodat het touw weer een meter langer wordt. Het touw is na dag 2 dus al 3 meter lang.
De volgende dag... affijn, het patroon is duidelijk. De hamvraag: bereikt de slak ooit B? Het verrassende antwoord is ja! Maar op welke dag?
Je hoeft geen rekening te houden met fysieke beperkingen of randvoorwaarden zoals de kromming van de aarde en dergelijke. De puzzel is puur wiskundig van aard.
Re: De slak op het elastiek
Kijk per dag naar het gedeelte van de afstand AB die de slak aflegt, en tel die afstand steeds bij het totaal (= het reeds afgelegde gedeelte) op.
Voorbeeld voor een snellere slak, die 50 cm per dag aflegt:
Dag 1 is het elastiek 100 cm, de slak legt 50 cm af, en is dan op 50/100 = de helft van AB, en omdat de slak juist gestart is, is dit ook de totale afstand na dag 1.
Dan wordt het elastiek 100 cm uitgerekt, maar daarmee blijft de slak op de helft van AB.
Dag 2 is het elastiek 200 cm, de slak legt 50 cm af, en is dan 50/200 deel van de afstand van AB dichter bij B, de totale afstand na dag 2 is dus 50/100 + 50/200 = 0.75 (= 75 % van de afstand)
Dan wordt het elastiek weer 100 cm uitgerekt, maar daarmee blijft de slak op de 0.75 van AB.
Dag 3 is het elastiek 300 cm, de slak legt 50 cm af, en is dan 50/300 deel van de afstand van AB dichter bij B, de totale afstand na dag 2 is dus 50/100 + 50/200 + 50/300 = 0.916666... (= 91.66 % van de afstand)
Dan wordt het elastiek weer 100 cm uitgerekt, maar daarmee blijft de slak op de 0.916666... van AB.
etc.
Merk op dat je de afgelegde afstand ook nog anders kan schrijven door 50/100 buiten haakjes te halen:
)
Kom je hiermee verder?
Voorbeeld voor een snellere slak, die 50 cm per dag aflegt:
Dag 1 is het elastiek 100 cm, de slak legt 50 cm af, en is dan op 50/100 = de helft van AB, en omdat de slak juist gestart is, is dit ook de totale afstand na dag 1.
Dan wordt het elastiek 100 cm uitgerekt, maar daarmee blijft de slak op de helft van AB.
Dag 2 is het elastiek 200 cm, de slak legt 50 cm af, en is dan 50/200 deel van de afstand van AB dichter bij B, de totale afstand na dag 2 is dus 50/100 + 50/200 = 0.75 (= 75 % van de afstand)
Dan wordt het elastiek weer 100 cm uitgerekt, maar daarmee blijft de slak op de 0.75 van AB.
Dag 3 is het elastiek 300 cm, de slak legt 50 cm af, en is dan 50/300 deel van de afstand van AB dichter bij B, de totale afstand na dag 2 is dus 50/100 + 50/200 + 50/300 = 0.916666... (= 91.66 % van de afstand)
Dan wordt het elastiek weer 100 cm uitgerekt, maar daarmee blijft de slak op de 0.916666... van AB.
etc.
Merk op dat je de afgelegde afstand ook nog anders kan schrijven door 50/100 buiten haakjes te halen:
Kom je hiermee verder?
Re: De slak op het elastiek
Is in de noemers de lengtes op verschillende dagen wel juist?
Ik zou voor dag twee schrijven, als je met relatieve afstanden wilt werken:
De slak heeft (50/200 + 50/200) deel = 1/2 deel van de afstand afgelegd. Vergelijkbaar voor elke dag is de helft van de afstand afgelegd.
Mochten we toch de lengtes op de verschillende dagen kunnen gebruiken, zou lenen makkelijk worden voor degene die leent.
Elke dag leen je €100 en betaal je €50 terug van de lening. Zonder verdere transacties, betaal als ooit af? Op het moment dat je hebt afbetaald, en je blijft hetzelfde lenen en terugbetalen als je deed, maak je dan nog schuld?
Numberphile op YouTube laat een vergelijkbare vraag met antwoord zien: https://youtu.be/4k1jegU4Wb4?t=3m
Misschien hangt het antwoord af van de context?
Ik zou voor dag twee schrijven, als je met relatieve afstanden wilt werken:
De slak heeft (50/200 + 50/200) deel = 1/2 deel van de afstand afgelegd. Vergelijkbaar voor elke dag is de helft van de afstand afgelegd.
Mochten we toch de lengtes op de verschillende dagen kunnen gebruiken, zou lenen makkelijk worden voor degene die leent.
Elke dag leen je €100 en betaal je €50 terug van de lening. Zonder verdere transacties, betaal als ooit af? Op het moment dat je hebt afbetaald, en je blijft hetzelfde lenen en terugbetalen als je deed, maak je dan nog schuld?
Numberphile op YouTube laat een vergelijkbare vraag met antwoord zien: https://youtu.be/4k1jegU4Wb4?t=3m
Misschien hangt het antwoord af van de context?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: De slak op het elastiek
Ik heb de beschrijving gevolgd, behalve de snelheid (ik nam een turbo-slak die 50 cm per dag aflegt).
Alle afstanden zijn in cm.
x_B = 100
x_slak = 0
x_B = 100
x_slak = 50 (voor de snelle slak)
relatieve positie van de slak ten opzichte van B: 50/100 = 0.50
x_B = 200
x_slak = 100 (de slak blijft op 50% van de totale afstand)
relatieve positie van de slak ten opzichte van B: 100/200 = 0.50
x_B = 200
x_slak = 150
vandaag afgelegd: 50/200
relatieve positie van de slak ten opzichte van B: 150/200 = 0.75
x_B = 300
x_slak = 225
relatieve positie van de slak ten opzichte van B: 225/300 = 0.75
Na dag 1 is de slak dus op relatieve positie 0.50:
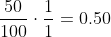
Na dag 2 op 0.75
 = 0.75)
etc
We zoeken dan de kleinste n zodanig dat
 \geq 1)
ofwel de kleinste n zodanig dat

en dit blijkt voor n=4.
Dus in 4 dagen is de snelle slak in punt B.
In je film benaderen ze dit met e^2 ~= 7, maar voor kleine getallen laat die benadering duidelijk nog te wensen over.
Alle afstanden zijn in cm.
x_A = 0antamaris schreef:Stel je voor: een touw van 1 meter lang. En niet zo maar een touw, nee: het bijzondere aan dit touw is dat het van elastiek is gemaakt dat je oneindig kunt uitrekken, zonder dat het breekt. De uiteinden van dit touw noemen we A en B. Het touw is bij A vastgemaakt. Tevens bevindt zich bij uiteinde A, hoe verrassend: een slak.
x_B = 100
x_slak = 0
x_A = 0antamaris schreef: Op een dag, laten we het dag 1 noemen, gebeurt er het volgende: de slak kruipt 50 cm richting B.
x_B = 100
x_slak = 50 (voor de snelle slak)
relatieve positie van de slak ten opzichte van B: 50/100 = 0.50
x_A = 0antamaris schreef: Gelijk hierna wordt er bij B aan het touw getrokken, zodat het touw 1 meter langer wordt.
x_B = 200
x_slak = 100 (de slak blijft op 50% van de totale afstand)
relatieve positie van de slak ten opzichte van B: 100/200 = 0.50
x_A = 0antamaris schreef: De volgende dag gebeurt er precies hetzelfde: de slak kruipt 50 cm richting B,
x_B = 200
x_slak = 150
vandaag afgelegd: 50/200
relatieve positie van de slak ten opzichte van B: 150/200 = 0.75
x_A = 0antamaris schreef: en er wordt opnieuw bij B getrokken, zodat het touw weer een meter langer wordt. Het touw is na dag 2 dus al 3 meter lang.
x_B = 300
x_slak = 225
relatieve positie van de slak ten opzichte van B: 225/300 = 0.75
Na dag 1 is de slak dus op relatieve positie 0.50:
Na dag 2 op 0.75
etc
We zoeken dan de kleinste n zodanig dat
ofwel de kleinste n zodanig dat
en dit blijkt voor n=4.
Dus in 4 dagen is de snelle slak in punt B.
In je film benaderen ze dit met e^2 ~= 7, maar voor kleine getallen laat die benadering duidelijk nog te wensen over.
Re: De slak op het elastiek
Ah, dat verklaart het voor me. Als het touw een meter wordt uitgerekt dan wordt de 'afgelegde' afstand door de slak ook groter. Die eigenschap van het touw had ik niet uit de omschrijving gelezen en niet uit het filmpje gevonden, maar is misschien wel wat je mag verwachten. Dank je wel!arie schreef:x_slak = 100 (de slak blijft op 50% van de totale afstand)
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: De slak op het elastiek
Bedankt voor de info en uitleg , maar ik zie het niet zitten.
Kunt U mij het antwoord geven dan ben ik allang blij.
Het is nl een vraag uit het GEOCACHE spel.
https://www.geocaching.com/geocache/GC6BX4F_de-slak
Vrgr Antamaris,
Kunt U mij het antwoord geven dan ben ik allang blij.
Het is nl een vraag uit het GEOCACHE spel.
https://www.geocaching.com/geocache/GC6BX4F_de-slak
Vrgr Antamaris,
Re: De slak op het elastiek
Op dit forum plaatsen we geen antwoorden op puzzels zoals geocache puzzels of puzzels van puzzelsites.
Dit is niet leuk voor de makers van deze puzzels, die er moeite en tijd voor nemen om hun puzzels te publiceren.
Aan de andere kant is het een zeer bekend wiskundig probleem, ruim terug te vinden op het net, en staat het antwoord bovendien al bijna hierboven:
Voor de slak die 50 cm per dag gaat zochten we de kleinste n zodanig dat



Voor de 50 cm/dag slak is het antwoord dus 4 dagen.
Voor een slak die 10 cm per dag gaat, zoeken we de kleinste n zodanig dat



Voor de 10 cm/dag slak is het antwoord dus 12367 dagen.
Met de hand optellen van al die breuken is niet te doen, maar dit kan weer via
http://www.wolframalpha.com/
Voer in het invoerveld in:
sum i=1 to 12366 (1.0 / i)
en je krijgt de optelling van die 12366 breuken: 9.9999621479...
Voer in het invoerveld in:
sum i=1 to 12367 (1.0 / i)
en je krijgt de optelling van die 12367 breuken: 10.000043008...
Voor jouw probleem, een slak die 5 cm per dag gaat, zoeken we de kleinste n zodanig dat

Je moet nu dus het getal n zoeken, zodanig dat
sum i=1 to n (1.0 / i)
net boven de 20 komt.
Nu is n een getal van 9 cijfers.
Lukt het je om dat met Wolfram Alpha te vinden?
Dit is niet leuk voor de makers van deze puzzels, die er moeite en tijd voor nemen om hun puzzels te publiceren.
Aan de andere kant is het een zeer bekend wiskundig probleem, ruim terug te vinden op het net, en staat het antwoord bovendien al bijna hierboven:
Voor de slak die 50 cm per dag gaat zochten we de kleinste n zodanig dat
Voor de 50 cm/dag slak is het antwoord dus 4 dagen.
Voor een slak die 10 cm per dag gaat, zoeken we de kleinste n zodanig dat
Voor de 10 cm/dag slak is het antwoord dus 12367 dagen.
Met de hand optellen van al die breuken is niet te doen, maar dit kan weer via
http://www.wolframalpha.com/
Voer in het invoerveld in:
sum i=1 to 12366 (1.0 / i)
en je krijgt de optelling van die 12366 breuken: 9.9999621479...
Voer in het invoerveld in:
sum i=1 to 12367 (1.0 / i)
en je krijgt de optelling van die 12367 breuken: 10.000043008...
Voor jouw probleem, een slak die 5 cm per dag gaat, zoeken we de kleinste n zodanig dat
Je moet nu dus het getal n zoeken, zodanig dat
sum i=1 to n (1.0 / i)
net boven de 20 komt.
Nu is n een getal van 9 cijfers.
Lukt het je om dat met Wolfram Alpha te vinden?
Re: De slak op het elastiek
Hoi allen,
Ter informatie : dit is een leuk maar bekend vraagstukje.
Zie b.v. op het internet : "Wiskunde Raadsels-hhofstede.nl." waar onder de deelvraag "De slak op het touw" zowat dezelfde vraag naar voren komt met antwoord.
Groetjes,
Parref.
Ter informatie : dit is een leuk maar bekend vraagstukje.
Zie b.v. op het internet : "Wiskunde Raadsels-hhofstede.nl." waar onder de deelvraag "De slak op het touw" zowat dezelfde vraag naar voren komt met antwoord.
Groetjes,
Parref.
Re: De slak op het elastiek
Je kan misschien ook kijken in de OEIS. Zoek eens naar 12367.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)


