Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Matrixrekenen, vectorruimten, groep-en ringstructuren, (lineaire) tranformaties.
-
barto
- Vergevorderde

- Berichten: 654
- Lid geworden op: 07 jun 2011, 16:02
Bericht
door barto » 25 jan 2012, 21:30
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 25 jan 2012, 21:48
Kan je 'vegen' ...
barto schreef:
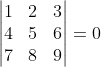
regel 2 - regel 1
regel 3 - regel 1
zie je iets bijzonders? Betekenis?
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 25 jan 2012, 21:52
Als Matrix B is ontstaan door een veelvoud van een rij dan wel kolom op te tellen bij een andere rij dan wel kolom van Matrix A, dan is de determinant van Matrix B gelijk aan de de determinant van Matrix A. (rij bij rij, kolom bij kolom).
Volgens mij volgt daaruit ook dat als je een matrix ziet als een stelsel van vergelijkingen (rechterzijden niet gegeven) dan heeft een inconsistent systeem determinant 0.
Kan je zo een 0-rij krijgen? Wat heb je aan een 0-rij?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
barto
- Vergevorderde

- Berichten: 654
- Lid geworden op: 07 jun 2011, 16:02
Bericht
door barto » 26 jan 2012, 16:56
David schreef:Kan je zo een 0-rij krijgen? Wat heb je aan een 0-rij?
bij

:
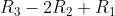
geeft

En dan is de determinant 0, door de nulrij.
bij
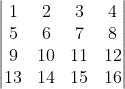
:
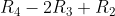
geeft
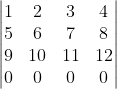
Algemeen, bij een
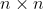
matrix wordt
+(R_n-2n)=0)
als

Dat was het dus denk ik.
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 26 jan 2012, 22:43
Ja, dat was het wel. Met de recursie om een det. te vinden, volgt dan dat een matrix met een nulrij en/of nulkolom een det. van 0 heeft.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)