Wiskundeforum

Ik denk van wel. Omdat er afgeleid wordt naar x, moet ook rekening gehouden worden met eventuele functies in x in de integratiegrenzen, en mag er niet enkel gekeken worden naar de integrand.

Nog even zeggen dat het goed werkt. Ik heb de functie g(x) ook partieel afgeleid naar y, en het resultaat komt opnieuw overeen met de gegeven oplossing.

Er geldt: g(x)=\int_{0}^{x}f(t)dt = F(x)-F(0) en dus is de afgeleide van g(x): \frac{d}{dx}(g(x)) = \frac{d}{dx}(F(x)-F(0)) = f(x) Als we nu de integratiegrenzen veranderen als volgt: g(x)=\int_{0}^{h(x)}f(t)dt = F(h(x)) - F(0) dan wordt de afgeleide van g(x): \frac{d}{dx}(g(x)) = \frac{d}{dx}(F(h(x...

Ik moet volgende afgeleide berekenen: \frac{\partial g}{\partial x} \mbox{, met } g(x,y,z)=\int_{4}^{x^2z}\frac{sin\left ( \frac{\pi yt}{24} \right )}{t}dt + \frac{cos(\frac{\pi xy}{4})}{\pi} Mijn oplossing was bijna juist, en ik begrijp niet waar de fout vandaan komt. Mijn oplossing was: \frac{\par...

Klopt, want er waren nog bijkomende gegevens (niet per se relevant voor mijn probleem).

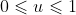De maximale hoogte is 1 (z=1). De gegeven vectoren zijn:



Dus .

Ik heb het gevonden. :idea: \begin{align*}\vec{pv} &= \vec{q} &\mbox{positievector} \\ \vec{rv} &= (\vec{q} - \vec{p}) &\mbox{richtingsvector} \end{align*} De parametrisatie is dus: \begin{align*} \vec{r} &= \vec{q} + u \cdot (\vec{q} - \vec{p}) \\ &= \vec{q} + u\vec{q} - u\vec{p} \\ &= (1-u)\vec{p}...

Wat betekenen pv en rv?

En die dimensie heb ik inderdaad over het hoofd gezien... Foutje

Gegeven zijn de punten P en Q met volgende parametervergelijking: \begin{align*} \vec{p} &= (\frac{1}{6}cos \frac{2 \pi t}{T}, \frac{1}{6}sin\frac{2 \pi t}{T}, 0) \\ \vec{q} &= (\frac{1}{3}cos \frac{2 \pi t}{T}, -\frac{1}{3}sin\frac{2 \pi t}{T},1) & \mbox{ met } 0\leqslant t \leqslant T\end{align*} ...

SafeX schreef:

Je kan toch delen ...

Hoe deel je deze veelterm?
Ik heb wat geprobeerd, maar het lukt mij niet...

Ik snap het! Door te vermenigvuldigen met (1-q) heffen n-1 termen elkaar op (bij de uitwerking) en verder is het niet moeilijk.

Enorm bedankt he.

Hallo iedereen,


ik begrijp een volgende stap niet bij een bepaalde berekening (i.v.m. reeksen):



Ik zie niet direct hoe je van de linkerkant naar de rechterkant geraakt...

Iemand een idee? Alvast bedankt.

Ik zie net in dat mijn vraag in feite geen steek houd. Ik vroeg mij af of je de basis gekozen voor V ook kon gebruiken als basis voor W. Wat ik net inzag (klopt dit?) is dat die bepaalde basis van V wél een basis kan zijn van een willekeurige vectorruimte W, zonder rekening te houden met de afbeeldi...

Ik was net een bewijs aan het bekijken van een stelling die zegt dat de dimensie van twee isomorfe, eindig voortgebrachte vectorruimten gelijk is. In het bewijs probeert men aan te tonen dat de verzameling van het beeld van de basisvectoren van de ene vectorruimte, de basis vormt van de andere vecto...

Een kolom vermenigvuldigen met een bepaald getal, zeg k, heeft tot gevolg dat je de waarde voor een bepaalde variabele deelt door k. In de uiteindelijke oplossing dien je dan de bekomen waarde te vermenigvuldigen met k. Uiteindelijk zijn delen en vermenigvuldigen redelijk analoge bewerkingen. Stel ...

Je reactie geeft me zeker een andere kijk (een nieuw inzicht) op het gegeven, en het maakt het deels (voor mij) verklaarbaar. :) Maar je geeft enkel een voorbeeld van de rijoperatie waarbij je een i-de kolom wisselt met een j-de kolom, terwijl er nog andere elementaire rijoperaties zijn (bij rijen a...