Hersenkraker! Wil werkende complexe formule omkeren
Hersenkraker! Wil werkende complexe formule omkeren
Ik heb de volgende goed werkende formule in excell,
Nwt =((($H$5/16/(2^(1/12)^9))*Len*Tot)^2*PI()*(ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5)))*(((Tot-Kern)/2)^2+Kern*(Tot-Kern)/2)+(F8^2*0,25*7,85))/((Tot-Kern)/2+Kern*0,5)^2)/(10^9)
Nu wil ik de formule omdraaien en Tot laten berekenen waarbij Nwt en de overige variabelen worden ingevoerd.
Dus
Tot = ...............
Ik heb geprobeerd de formule in delen op te splitsen maar krijg het niet voor elkaar.
Alvast bedankt voor jullie hulp!
Nwt =((($H$5/16/(2^(1/12)^9))*Len*Tot)^2*PI()*(ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5)))*(((Tot-Kern)/2)^2+Kern*(Tot-Kern)/2)+(F8^2*0,25*7,85))/((Tot-Kern)/2+Kern*0,5)^2)/(10^9)
Nu wil ik de formule omdraaien en Tot laten berekenen waarbij Nwt en de overige variabelen worden ingevoerd.
Dus
Tot = ...............
Ik heb geprobeerd de formule in delen op te splitsen maar krijg het niet voor elkaar.
Alvast bedankt voor jullie hulp!
Re: Hersenkraker! Wil werkende complexe formule omkeren
Als dit je formule is:
/2)^2 + kern \cdot (tot-kern)/2 \right} + F_8^2 \cdot 1.9625 \right]}{10^9 \cdot ((tot-kern)/2+kern/2)^2})
dan is (vermenigvuldig met 10^9 en werk de noemer uit):
/2)^2 + kern \cdot (tot-kern)/2 \right} + F_8^2 \cdot 1.9625 \right]}{(tot/2-kern/2+kern/2)^2})
ofwel
/2)^2 + kern \cdot (tot-kern)/2 \right} + F_8^2 \cdot 1.9625 \right]}{(tot/2)^2})
ofwel
/2)^2 + kern \cdot (tot-kern)/2 \right} + F_8^2 \cdot 1.9625 \right]}{(tot)^2})
en nu valt tot^2 in de noemer weg tegen tot^2 in de teller (eerste breuk in de teller):
/2)^2 + kern \cdot (tot-kern)/2 \right} + F_8^2 \cdot 1.9625 \right])
herleid dan het deel tussen de accolades:
/2) + kern \right] \cdot (tot-kern)/2 \right} + F_8^2 \cdot 1.9625 \right])
ofwel:
/2) \right] \cdot (tot-kern)/2 \right} + F_8^2 \cdot 1.9625 \right])
ofwel:
/4 \right} + F_8^2 \cdot 1.9625 \right])
ofwel:
 + 4 \cdot F_8^2 \cdot 1.9625 \right])
en hieruit kan je tot^2 oplossen, daarna weet je ook tot.
NOOT: heb ik je formule goed gelezen/vertaald??
dan is (vermenigvuldig met 10^9 en werk de noemer uit):
ofwel
ofwel
en nu valt tot^2 in de noemer weg tegen tot^2 in de teller (eerste breuk in de teller):
herleid dan het deel tussen de accolades:
ofwel:
ofwel:
ofwel:
en hieruit kan je tot^2 oplossen, daarna weet je ook tot.
NOOT: heb ik je formule goed gelezen/vertaald??
Re: Hersenkraker! Wil werkende complexe formule omkeren
Hallo Arie,
Hartelijk dank voor je reactie!
Ik kan niet goed beoordelen of je de formule correct hebt omschreven.
Misschien is het handig als ik een voorbeeld excell bestand toevoeg.
In het bovenste deel wordt Nwt berekend met een paar voorbeelden
In het onderste deel heb ik dus de omgekeerde formule nodig om Tot te berekenen.
Zou je de formule in het onderste deel kunnen zetten? Wanneer dezelfde waardes berekend worden klopt de omgekeerde formule lijkt me.
Wederom dank voor je reactie!
hmm, het toevoegen van een bijlage lukt niet omdat de forum blijlagen quota is bereikt....
Kan ik het bestand naar je emailen?
Hartelijk dank voor je reactie!
Ik kan niet goed beoordelen of je de formule correct hebt omschreven.
Misschien is het handig als ik een voorbeeld excell bestand toevoeg.
In het bovenste deel wordt Nwt berekend met een paar voorbeelden
In het onderste deel heb ik dus de omgekeerde formule nodig om Tot te berekenen.
Zou je de formule in het onderste deel kunnen zetten? Wanneer dezelfde waardes berekend worden klopt de omgekeerde formule lijkt me.
Wederom dank voor je reactie!
hmm, het toevoegen van een bijlage lukt niet omdat de forum blijlagen quota is bereikt....
Kan ik het bestand naar je emailen?
Re: Hersenkraker! Wil werkende complexe formule omkeren
Als mijn vorige post goed is, dan moet deze vergelijking dezelfde waarden voor Nwt leveren als de formule die jij gaf:
Nwt = PI()*($H$5*Len/26,90868529)^2*(ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5)))*(Tot^2-Kern^2)+7,85*F8^2)/(10^9)
Als dat zo is, dan is
Tot^2 = (((10^9)*Nwt/(PI()*($H$5*Len/26,90868529)^2)-7,85*F8^2)/ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5))))+Kern^2
dus (als Tot positief is):
Tot = WORTEL((((10^9)*Nwt/(PI()*($H$5*Len/26,90868529)^2)-7,85*F8^2)/ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5))))+Kern^2)
(het kan zijn dat je in plaats van WORTEL iets als SQRT moet gebruiken).
Met deze formule zou je, als Nwt en de overige waarden gegeven zijn, Tot moeten kunnen berekenen.
Je kan dit zelf testen.
Indien bovenstaande niet klopt, dan is het het handigst om op dit forum een paar voorbeelden te geven.
Wat in dat geval nodig is zijn:
- de waarden van de constanten:
H5
P3
P4
P5
- een beperkt aantal (zeg 3 tot 5) voorbeelden van bij elkaar horende waarden van:
Nwt
E8
F8
Len
Tot
Kern
Nwt = PI()*($H$5*Len/26,90868529)^2*(ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5)))*(Tot^2-Kern^2)+7,85*F8^2)/(10^9)
Als dat zo is, dan is
Tot^2 = (((10^9)*Nwt/(PI()*($H$5*Len/26,90868529)^2)-7,85*F8^2)/ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5))))+Kern^2
dus (als Tot positief is):
Tot = WORTEL((((10^9)*Nwt/(PI()*($H$5*Len/26,90868529)^2)-7,85*F8^2)/ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5))))+Kern^2)
(het kan zijn dat je in plaats van WORTEL iets als SQRT moet gebruiken).
Met deze formule zou je, als Nwt en de overige waarden gegeven zijn, Tot moeten kunnen berekenen.
Je kan dit zelf testen.
Indien bovenstaande niet klopt, dan is het het handigst om op dit forum een paar voorbeelden te geven.
Wat in dat geval nodig is zijn:
- de waarden van de constanten:
H5
P3
P4
P5
- een beperkt aantal (zeg 3 tot 5) voorbeelden van bij elkaar horende waarden van:
Nwt
E8
F8
Len
Tot
Kern
Re: Hersenkraker! Wil werkende complexe formule omkeren
Ik heb jouw formule in excell gezet en hij werkt bijna perfect!!
Wanneer E8 (i/m/k) echter leeg is geeft hij een foutmelding (delen door 0)
Mijn rekenvoorbeelden:
hier wordt Nwt berekend
Len i/m/k Kern Tot Nwt
1200 i 1,200 6,000 266
1000 m 1,200 5,500 171
800 k 1,200 5,000 95
8000 1,200 4,000 608
hier wordt Tot berekend
Len i/m/k Kern Tot Nwt
1200 i 1,200 6,000 266
1000 m 1,200 5,500 171
800 k 1,200 5,000 95
8000 1,200 #DEEL/0! 608
De waardes voor i/m/k:
i = 6,039
m = 6,691
k = 6,99
$H$5 = 440
In bovenstaand voorbeeld zou de laatse variant (met len = 8000 en i/m/k is leeg) dus een Tot op moeten leveren van 4,000
Nogmaals dank voor je hulp!
ps. In het reactieveld waar ik dit in typ zien de voorbeelden er netjes uit maar kennelijk veranderd de opmaak als ik de post plaats. Ik hoop dat het duidelijk is
Wanneer E8 (i/m/k) echter leeg is geeft hij een foutmelding (delen door 0)
Mijn rekenvoorbeelden:
hier wordt Nwt berekend
Len i/m/k Kern Tot Nwt
1200 i 1,200 6,000 266
1000 m 1,200 5,500 171
800 k 1,200 5,000 95
8000 1,200 4,000 608
hier wordt Tot berekend
Len i/m/k Kern Tot Nwt
1200 i 1,200 6,000 266
1000 m 1,200 5,500 171
800 k 1,200 5,000 95
8000 1,200 #DEEL/0! 608
De waardes voor i/m/k:
i = 6,039
m = 6,691
k = 6,99
$H$5 = 440
In bovenstaand voorbeeld zou de laatse variant (met len = 8000 en i/m/k is leeg) dus een Tot op moeten leveren van 4,000
Nogmaals dank voor je hulp!
ps. In het reactieveld waar ik dit in typ zien de voorbeelden er netjes uit maar kennelijk veranderd de opmaak als ik de post plaats. Ik hoop dat het duidelijk is
Re: Hersenkraker! Wil werkende complexe formule omkeren
Excuses,
Ik kom er net achter dat mijn redenatie niet klopt.
Wanneer in het eerste deel, dus Nwt wordt berekend, het veld i/m/k leeg is heeft Tot geen enkel effect.
Ik had daar 4,000 ingevuld, maar die waarde doet daar niet mee.
In dat geval wordt alleen Kern meegenomen in de berekening
Dus moet de omgekeerde formule ook geen 4,000 opleveren, maar 1,200
Het grappige is dat wanneer je wel iets invult voor i/m/k, er altijd keurig 1,200 uit komt voor Tot!!
Dus de vraag nu is hoe ik bij een leeg veld i/m/k de uitkomst Tot gelijk aan Kern krijg
Ik hoop dat het zo duidelijk is
Ik kom er net achter dat mijn redenatie niet klopt.
Wanneer in het eerste deel, dus Nwt wordt berekend, het veld i/m/k leeg is heeft Tot geen enkel effect.
Ik had daar 4,000 ingevuld, maar die waarde doet daar niet mee.
In dat geval wordt alleen Kern meegenomen in de berekening
Dus moet de omgekeerde formule ook geen 4,000 opleveren, maar 1,200
Het grappige is dat wanneer je wel iets invult voor i/m/k, er altijd keurig 1,200 uit komt voor Tot!!
Dus de vraag nu is hoe ik bij een leeg veld i/m/k de uitkomst Tot gelijk aan Kern krijg
Ik hoop dat het zo duidelijk is
Re: Hersenkraker! Wil werkende complexe formule omkeren
Klopt, hierboven hadden we:
 + 7.85 \cdot F_8^2 \right] / 10^9)
waarbij constante gamma_imk afhankelijk is van i, m of k.
Als i, m of k niet gegeven zijn, wordt in Excel gamma_imk = 0, en gaat de formule over in:
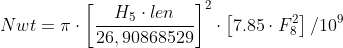
dus onafhankelijk van Tot.
(overigens: ik neem aan dat F8 = Kern, klopt dat?)
In je voorbeeld hierboven:
Indien je voor gamma_imk ongedefinieerd Tot gelijk wil maken aan de Kern, dan kan je de hele formule in een ALS constructie plaatsen:
Tot = ALS(E8="";Kern;WORTEL((((10^9)*Nwt/(PI()*($H$5*Len/26,90868529)^2)-7,85*F8^2)/ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5))))+Kern^2))
Dit lees je:
als E8 leeg is (= twee dubbele aanhalingstekens achter elkaar):
ALS(E8=""
dan: maak het resultaat Tot gelijk aan de Kern:
;Kern
anders: maak het resultaat gelijk aan de wortel:
;WORTEL((((10^9)*Nwt/(PI()*($H$5*Len/26,90868529)^2)-7,85*F8^2)/ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5))))+Kern^2))
waarbij constante gamma_imk afhankelijk is van i, m of k.
Als i, m of k niet gegeven zijn, wordt in Excel gamma_imk = 0, en gaat de formule over in:
dus onafhankelijk van Tot.
(overigens: ik neem aan dat F8 = Kern, klopt dat?)
In je voorbeeld hierboven:
Code: Selecteer alles
Len i/m/k Kern Tot Nwt
8000 1,200 4,000 608
8000 1,200 5,000 608
8000 1,200 1,234 608
Tot = ALS(E8="";Kern;WORTEL((((10^9)*Nwt/(PI()*($H$5*Len/26,90868529)^2)-7,85*F8^2)/ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5))))+Kern^2))
Dit lees je:
als E8 leeg is (= twee dubbele aanhalingstekens achter elkaar):
ALS(E8=""
dan: maak het resultaat Tot gelijk aan de Kern:
;Kern
anders: maak het resultaat gelijk aan de wortel:
;WORTEL((((10^9)*Nwt/(PI()*($H$5*Len/26,90868529)^2)-7,85*F8^2)/ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5))))+Kern^2))
Re: Hersenkraker! Wil werkende complexe formule omkeren
Ik begrijp nu hoe i/m/k irrelevant wordt wanneer Nwt wordt berekend
Bedankt voor de uitleg!
Overigens is F8 inderdaad Kern
Mijn bedoeling bij de omgekeerde formule, Tot wordt berekend, is eigenlijk dat wanneer i/m/k leeg is de uitkomst gelijk is aan de ingevulde Kern (en leeg i/m/k) bij de Nwt berekening.
In ons voorbeeld dus die 1,200
Nu wordt die 1,200 keurig berekend wanneer er iets, maakt niet uit wat, ingevuld wordt voor i/m/k
Kan ik ongestrafd in excell een waarde aan i/m/k toekennen wanneer deze leeg wordt gelaten?
Ik heb voor de cel i/m/k nu een keuzelijst gemaakt waarbij de constante geselecteerd wordt afhankelijk van de keuze:
Keuzes:
i = 6,039
m = 6,691
k = 6,99
Ik kan daar een lege keuze bij maken die bijvoorbeeld de waarde 1 heeft (deze doet er dus eigenlijk niet toe maar voorkomt een foutmelding delen door 0)
Dus als i/m/k is leeg, dan heeft hij een waarde van 1
Dan wordt keurig de Tot uitgerekend die gelijk is aan de Kern in de omgedraaide versie, en kan ik dus Kern bepalen wanneer i/m/k leeg is door voor kern te stellen dat ALS i/m/k is leeg (of"") dan Kern = Tot
Daar zal dan nog een kleine stap achter moeten om voor kern de dichtstbijliggende maat uit een lijst bestaande kernmaten te zoeken, waarna de uiteindelijke Nwt (in een eigen kolom) weer berekend kan worden aan de hand van de opgezochte kernmaat.
Het gaat hier om een excell met veel rijen die elk een iets andere formule hebben voor Nwt.
Als we deze eerste correct hebben omgezet zal ik proberen de variaties te herleiden.
De volgende heeft bijvoorbeel $H$5/16/(2^(1/12)^8 waar we nu $H$5/16/(2^(1/12)^9 hadden
Ik neem aan dat die 26,90868529 daardoor veranderd?
Bedankt voor de uitleg!
Overigens is F8 inderdaad Kern
Mijn bedoeling bij de omgekeerde formule, Tot wordt berekend, is eigenlijk dat wanneer i/m/k leeg is de uitkomst gelijk is aan de ingevulde Kern (en leeg i/m/k) bij de Nwt berekening.
In ons voorbeeld dus die 1,200
Nu wordt die 1,200 keurig berekend wanneer er iets, maakt niet uit wat, ingevuld wordt voor i/m/k
Kan ik ongestrafd in excell een waarde aan i/m/k toekennen wanneer deze leeg wordt gelaten?
Ik heb voor de cel i/m/k nu een keuzelijst gemaakt waarbij de constante geselecteerd wordt afhankelijk van de keuze:
Keuzes:
i = 6,039
m = 6,691
k = 6,99
Ik kan daar een lege keuze bij maken die bijvoorbeeld de waarde 1 heeft (deze doet er dus eigenlijk niet toe maar voorkomt een foutmelding delen door 0)
Dus als i/m/k is leeg, dan heeft hij een waarde van 1
Dan wordt keurig de Tot uitgerekend die gelijk is aan de Kern in de omgedraaide versie, en kan ik dus Kern bepalen wanneer i/m/k leeg is door voor kern te stellen dat ALS i/m/k is leeg (of"") dan Kern = Tot
Daar zal dan nog een kleine stap achter moeten om voor kern de dichtstbijliggende maat uit een lijst bestaande kernmaten te zoeken, waarna de uiteindelijke Nwt (in een eigen kolom) weer berekend kan worden aan de hand van de opgezochte kernmaat.
Het gaat hier om een excell met veel rijen die elk een iets andere formule hebben voor Nwt.
Als we deze eerste correct hebben omgezet zal ik proberen de variaties te herleiden.
De volgende heeft bijvoorbeel $H$5/16/(2^(1/12)^8 waar we nu $H$5/16/(2^(1/12)^9 hadden
Ik neem aan dat die 26,90868529 daardoor veranderd?
Re: Hersenkraker! Wil werkende complexe formule omkeren
Als het goed is dan doet de formule in mijn laatste post dat:formule schreef:Mijn bedoeling bij de omgekeerde formule, Tot wordt berekend, is eigenlijk dat wanneer i/m/k leeg is de uitkomst gelijk is aan de ingevulde Kern (en leeg i/m/k) bij de Nwt berekening.
In ons voorbeeld dus die 1,200
Nu wordt die 1,200 keurig berekend wanneer er iets, maakt niet uit wat, ingevuld wordt voor i/m/k
ALS E8 leeg is (dus niets ingevuld in de kolom met "i", "m" of "k"), toon dan de waarde van Kern, en in alle andere gevallen: bereken onze oorspronkelijke wortel.
Alleen als die waarde niet gebruikt wordt in de verdere berekening. Als die waarde wel gebruikt wordt, dan zal Excel automatisch ook de toegekende waarde gebruiken.formule schreef: Kan ik ongestraft in excell een waarde aan i/m/k toekennen wanneer deze leeg wordt gelaten?
Dit gaat mis. Neem de oorspronkelijke formule:formule schreef: Ik heb voor de cel i/m/k nu een keuzelijst gemaakt waarbij de constante geselecteerd wordt afhankelijk van de keuze:
Keuzes:
i = 6,039
m = 6,691
k = 6,99
Ik kan daar een lege keuze bij maken die bijvoorbeeld de waarde 1 heeft (deze doet er dus eigenlijk niet toe maar voorkomt een foutmelding delen door 0)
Dus als i/m/k is leeg, dan heeft hij een waarde van 1
dus
Als i, m of k niet gegeven is, dan maakt Excel de constante gamma_imk gelijk aan nul.
In de formule voor Nwt gaat dat goed: gamma_imk * (tot^2 - kern^2) wordt nul, en Excel rekent daarmee verder om Nwt te bepalen.
In de formule voor tot^2 gaat het mis omdat daar gedeeld wordt door gamma_imk.
Als je de deling door nul wilt omzeilen door gamma_imk in dat geval gelijk aan 1 te maken, dan wordt de formule:
ofwel
Nu is je deling door nul voorkomen, maar hebben we het volgende probleem: in het algemeen zal Tot nu niet gelijk zijn aan Kern.
Je kan dat wel opvangen door een nieuwe constante delta te definieren:
dus
en definieer nu delta, zo dat
waarbij:
delta(i) = 1 / gamma(i) = 1 / 6,039
delta(m) = 1 / gamma(m) = 1 / 6,691
delta(k) = 1 / gamma(k) = 1 / 6,99
delta("") = 0
Als i, m of k niet gegeven zijn, wordt delta nul en wordt
tot^2 = kern^2
ofwel (beide positief):
tot = kern
In je Excel blad kan je dit ( voor je regel 8 ) vertalen naar:
ALS(E8="i";1/$P$3;ALS(E8="m";1/$P$4;ALS(E8="k";1/$P$5;0)))
(je kan deze formule ook in een vrije kolom plaatsen en dan in je andere formules naar de betreffende cel verwijzen).
Klopt, ik heb dit in de formules hierboven aangepast.formule schreef: De volgende heeft bijvoorbeel $H$5/16/(2^(1/12)^8 waar we nu $H$5/16/(2^(1/12)^9 hadden
Ik neem aan dat die 26,90868529 daardoor veranderd?
Re: Hersenkraker! Wil werkende complexe formule omkeren
Wederom hartelijk dank voor je antwoord en uitleg!
Ik doe mijn best je te volgen en de nieuwe versie voor Tot berekening in excell te vertalen.
Ik heb nu:
Tot =WORTEL(ALS(E26="i";1/$P$3;ALS(E26="m";1/$P$4;ALS(E26="k";1/$P$5;0)))
*(((10^9)*I26)/(PI()*(16*2^(9/12)/($H$5*D26)))-(7,85*F26^2)+(F26^2)))
waarbij E26 = i/m/k, I26 = Nwt, D26 = Len en F26 = Kern
Maar dat gaat niet goed, wanneer i/m/k een waarde heeft geeft hij delen door 0 fout. Bij i/m/k is leeg geeft hij #waarde
Voor alle duidelijkheid,
Bij het berekenen wil ik in het geval van i/m/k is ingevuld dat hij Tot geeft (werkt perfect met jouw 1e formule!)
Maar wanneer i/m/k is leeg, dan wil ik Kern berekend hebben, deze is echter altijd gelijk aan Tot wanneer i/m/k leeg is, vandaar mijn voorstel om Kern = Tot te doen in dat geval.
Dat heb ik eerder niet goed omschreven wellicht, door te stellen dat Tot = Kern (alsof ik Kern op ga geven wanneer i/m/k leeg is)
Ik doe mijn best je te volgen en de nieuwe versie voor Tot berekening in excell te vertalen.
Ik heb nu:
Tot =WORTEL(ALS(E26="i";1/$P$3;ALS(E26="m";1/$P$4;ALS(E26="k";1/$P$5;0)))
*(((10^9)*I26)/(PI()*(16*2^(9/12)/($H$5*D26)))-(7,85*F26^2)+(F26^2)))
waarbij E26 = i/m/k, I26 = Nwt, D26 = Len en F26 = Kern
Maar dat gaat niet goed, wanneer i/m/k een waarde heeft geeft hij delen door 0 fout. Bij i/m/k is leeg geeft hij #waarde
Voor alle duidelijkheid,
Bij het berekenen wil ik in het geval van i/m/k is ingevuld dat hij Tot geeft (werkt perfect met jouw 1e formule!)
Maar wanneer i/m/k is leeg, dan wil ik Kern berekend hebben, deze is echter altijd gelijk aan Tot wanneer i/m/k leeg is, vandaar mijn voorstel om Kern = Tot te doen in dat geval.
Dat heb ik eerder niet goed omschreven wellicht, door te stellen dat Tot = Kern (alsof ik Kern op ga geven wanneer i/m/k leeg is)
Re: Hersenkraker! Wil werkende complexe formule omkeren
Je formule lijkt me niet helemaal te kloppen.
Ik kom uit op:
Tot = WORTEL( ALS(E26="i";1/$P$3;ALS(E26="m";1/$P$4;ALS(E26="k";1/$P$5;0))) * ( ((10^9)*I26/PI()) * (16*2^(9/12)/($H$5*D26))^2 - 7,85*F26^2) + F26^2 )
Als het goed is geeft dit hetzelfde resultaat als mijn eerdere Tot formule.
Ik nam aan dat je bedoelde dat Tot gelijk moet worden aan Kern als i/m/k leeg is, en dat gebeurt hierboven.
Als je daarentegen Kern gelijk wil maken aan Tot als i/m/k leeg is, dan moet Tot in dat geval bekend zijn.
Indien je dat allemaal in 1 kolom wil, krijg je zo'n soort constructie:
Resultaat = ALS( OF(E26="i";E26="m";E26="k") ; [wortelformule] ; Tot )
waarbij [wortelformule] de formule is om Tot te berekenen (die nu iets vereenvoudigd kan worden):
Resultaat = ALS( OF(E26="i";E26="m";E26="k") ; WORTEL( ( ((10^9)*I26/PI()) * (16*2^(9/12)/($H$5*D26))^2 - 7,85*F26^2) / ALS(E26="i";$P$3;ALS(E26="m";$P$4;$P$5)) + F26^2 ) ; Tot )
Als E26 gelijk is aan i, m of k, dan wordt Tot berekend met de formule, zo niet, dan wordt de al bekende waarde van Tot teruggegeven.
Bedoel je dit?
Ik kom uit op:
Tot = WORTEL( ALS(E26="i";1/$P$3;ALS(E26="m";1/$P$4;ALS(E26="k";1/$P$5;0))) * ( ((10^9)*I26/PI()) * (16*2^(9/12)/($H$5*D26))^2 - 7,85*F26^2) + F26^2 )
Als het goed is geeft dit hetzelfde resultaat als mijn eerdere Tot formule.
Ik nam aan dat je bedoelde dat Tot gelijk moet worden aan Kern als i/m/k leeg is, en dat gebeurt hierboven.
Als je daarentegen Kern gelijk wil maken aan Tot als i/m/k leeg is, dan moet Tot in dat geval bekend zijn.
Indien je dat allemaal in 1 kolom wil, krijg je zo'n soort constructie:
Resultaat = ALS( OF(E26="i";E26="m";E26="k") ; [wortelformule] ; Tot )
waarbij [wortelformule] de formule is om Tot te berekenen (die nu iets vereenvoudigd kan worden):
Resultaat = ALS( OF(E26="i";E26="m";E26="k") ; WORTEL( ( ((10^9)*I26/PI()) * (16*2^(9/12)/($H$5*D26))^2 - 7,85*F26^2) / ALS(E26="i";$P$3;ALS(E26="m";$P$4;$P$5)) + F26^2 ) ; Tot )
Als E26 gelijk is aan i, m of k, dan wordt Tot berekend met de formule, zo niet, dan wordt de al bekende waarde van Tot teruggegeven.
Bedoel je dit?
Re: Hersenkraker! Wil werkende complexe formule omkeren
Dat is niet helemaal wat ik bedoel.
Misschien moet ik wat uitleg geven over wat er wordt berekend om het duidelijker over te kunnen brengen.
De berekeningen hebben betrekking op een stalen cylinder met al dan niet een materiaal daaromheen gewikkeld (i, m of k)
De stalen cylinder is de Kern, er is altijd een kern (met soortelijke massa 7,85)
Soms zal de kern dus omwikkeld zijn met materiaal i,m of k (hun soortelijk gewicht zijn de constanten in het rijtje $P$3 t/m $P$5)
Nu wil ik de kracht opgeven en de totaaldikte en kerndikte bepalen. De totaaldikte wordt berekend door jouw formule. Deze zal zolang er geen Kern is ingevuld de benodigde dikte berekenen afhankelijk van het gekozen materiaal bij i/m/k.
Vervolgens vul ik zelf een Kerndikte in, hierdoor veranderd de totaaldikte weer iets aangezien de kern een ander soortelijk gewicht heeft en een deel van de totaaldikte is.
Tot zover perfect!
Nu wil ik echter de diameter van een stalen cylinder (Kern) zonder extra omwikkel materiaal (dus i/m/k is leeg) berekenen door oa de kracht (Nwt) op te geven. Het hele i/m/k gedeelte vervalt dan dus aangezien er geen materiaal aan de kern wordt toegevoegd, dus daarvan hoeven we dan ook de massa niet te berekenen.
Vandaar ook dat in de orginele formule (waar Nwt wordt berekend) het gedeelte i/m/k geen invloed heeft wanneer die leeg is. Dan wordt er enkel gerekend met die 7,85 omdat de hele cylinder van staal is.
Mijn redenatie is dus als volgt:
Wanneer er geen materiaal aan de stalen kern wordt toegevoegd (i/m/k is leeg) zou de formule voor het berekenen van Tot(aaldikte) een Tot moeten berekenen gebaseerd op enkel die 7,85. Het deel i/m/k doet dan niet mee.
Deze berekende Tot is nu dus gelijk aan Kern of misschien beter gezegd als Tot berkend is kan ik stellen dat Kern = Tot (aangevuld met een bestaande kernmaat opzoeken maar daar kom ik wel uit)
Het enige probleem met de formule voor Tot berekenen is dus dat hij geen Tot berekend wanneer i/m/k leeg is.
Ik hoop dat het zo duidelijk is
Ik vind het super hoe je me helpt!
Misschien moet ik wat uitleg geven over wat er wordt berekend om het duidelijker over te kunnen brengen.
De berekeningen hebben betrekking op een stalen cylinder met al dan niet een materiaal daaromheen gewikkeld (i, m of k)
De stalen cylinder is de Kern, er is altijd een kern (met soortelijke massa 7,85)
Soms zal de kern dus omwikkeld zijn met materiaal i,m of k (hun soortelijk gewicht zijn de constanten in het rijtje $P$3 t/m $P$5)
Nu wil ik de kracht opgeven en de totaaldikte en kerndikte bepalen. De totaaldikte wordt berekend door jouw formule. Deze zal zolang er geen Kern is ingevuld de benodigde dikte berekenen afhankelijk van het gekozen materiaal bij i/m/k.
Vervolgens vul ik zelf een Kerndikte in, hierdoor veranderd de totaaldikte weer iets aangezien de kern een ander soortelijk gewicht heeft en een deel van de totaaldikte is.
Tot zover perfect!
Nu wil ik echter de diameter van een stalen cylinder (Kern) zonder extra omwikkel materiaal (dus i/m/k is leeg) berekenen door oa de kracht (Nwt) op te geven. Het hele i/m/k gedeelte vervalt dan dus aangezien er geen materiaal aan de kern wordt toegevoegd, dus daarvan hoeven we dan ook de massa niet te berekenen.
Vandaar ook dat in de orginele formule (waar Nwt wordt berekend) het gedeelte i/m/k geen invloed heeft wanneer die leeg is. Dan wordt er enkel gerekend met die 7,85 omdat de hele cylinder van staal is.
Mijn redenatie is dus als volgt:
Wanneer er geen materiaal aan de stalen kern wordt toegevoegd (i/m/k is leeg) zou de formule voor het berekenen van Tot(aaldikte) een Tot moeten berekenen gebaseerd op enkel die 7,85. Het deel i/m/k doet dan niet mee.
Deze berekende Tot is nu dus gelijk aan Kern of misschien beter gezegd als Tot berkend is kan ik stellen dat Kern = Tot (aangevuld met een bestaande kernmaat opzoeken maar daar kom ik wel uit)
Het enige probleem met de formule voor Tot berekenen is dus dat hij geen Tot berekend wanneer i/m/k leeg is.
Ik hoop dat het zo duidelijk is
Ik vind het super hoe je me helpt!
Re: Hersenkraker! Wil werkende complexe formule omkeren
Dan gaat het je om de derde factor in:
 + 7.85 \cdot kern^2 \right] / 10^9)
dat is
 + 7.85 \cdot kern^2 \right])
Als er geen omhullend materiaal is, dan is tot = kern, en wordt deze factor

Deze situatie heb je opgelost door gamma_imk = nul te maken als geen i, m of k gegeven zijn.
Voor berekening van Nwt uit tot, kern, etc, is dit correct.
Voor de berekening van tot uit Nwt, kern, etc, ging dit mis omdat we door gamma_imk moesten delen.
Daarom is het handiger om gamma_imk = 7,85 te maken als er geen i, m of k omhulling is.
In dat geval is weer tot = kern, en wordt de bovenstaande factor:
 + 7.85 \cdot kern^2 \right])


en omdat tot = kern

en dit is wat we zochten, zonder dat gamma_imk nul wordt.
De formule voor Nwt kunnen we dus ook schrijven als:
Nwt = PI()*($H$5*Len/(16*2^(9/12))^2*(ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5;7,85)))*(Tot^2-Kern^2)+7,85*Kern^2)/(10^9)
Merk op dat we in de derde ALS() nu de waarde 7,85 hebben staan, die wordt gekozen als aan geen van de andere gevallen (E8 = i, m of k) is voldaan.
De formule

verandert met gamma_imk = 7.85 (dus als geen i, m of k zijn ingevuld) in:



Nu kan je tot berekenen uit Nwt terwijl je kern niet nodig hebt.
In Excel stijl:
Tot = WORTEL( ( ((10^9)*I26/PI()) * (16*2^(9/12)/($H$5*D26))^2 - 7,85*F26^2) / ALS(E26="i";$P$3;ALS(E26="m";$P$4;ALS(E26="k";$P$5;7,85))) + F26^2 )
Let ook hier weer op de toegevoegde 7,85 in de derde ALS()
Het kan zijn dat Excel moeilijk doet (= foutmelding geeft) over een niet ingevulde F26 = kern waarde in het geval geen i/m/k. In dat geval kan je de kern elke waarde, bv nul, geven, deze waarde valt toch automatisch weg in de formule (het gedeelte -kern^2+kern^2 onder de herschreven wortel).
Het alternatief is een zeer lange formule, waarin je onderscheid maakt tussen wel of geen i/m/k:
Tot =
ALS( OF(E28="i";E28="m";E28="k");
WORTEL( ( ((10^9)*I26/PI()) * (16*2^(9/12)/($H$5*D26))^2 - 7,85*F26^2) / ALS(E26="i";$P$3;ALS(E26="m";$P$4;$P$5)) + F26^2 );
WORTEL( ( (10^9)*I26/(7,85*PI()) ) * (16*2^(9/12)/($H$5*D26))^2 ) )
Indien er i/m/k gedefinieerd is, gebruikt Excel de eerste formule,
anders de gereduceerde formule met gamma_imk = 7,85.
Hierdoor voorkom je een #WAARDE foutmelding als Kern en i/m/k beide niet gegeven zijn.
Kom je hiermee verder?
dat is
Als er geen omhullend materiaal is, dan is tot = kern, en wordt deze factor
Deze situatie heb je opgelost door gamma_imk = nul te maken als geen i, m of k gegeven zijn.
Voor berekening van Nwt uit tot, kern, etc, is dit correct.
Voor de berekening van tot uit Nwt, kern, etc, ging dit mis omdat we door gamma_imk moesten delen.
Daarom is het handiger om gamma_imk = 7,85 te maken als er geen i, m of k omhulling is.
In dat geval is weer tot = kern, en wordt de bovenstaande factor:
en omdat tot = kern
en dit is wat we zochten, zonder dat gamma_imk nul wordt.
De formule voor Nwt kunnen we dus ook schrijven als:
Nwt = PI()*($H$5*Len/(16*2^(9/12))^2*(ALS(E8="i";$P$3;ALS(E8="m";$P$4;ALS(E8="k";$P$5;7,85)))*(Tot^2-Kern^2)+7,85*Kern^2)/(10^9)
Merk op dat we in de derde ALS() nu de waarde 7,85 hebben staan, die wordt gekozen als aan geen van de andere gevallen (E8 = i, m of k) is voldaan.
De formule
verandert met gamma_imk = 7.85 (dus als geen i, m of k zijn ingevuld) in:
Nu kan je tot berekenen uit Nwt terwijl je kern niet nodig hebt.
In Excel stijl:
Tot = WORTEL( ( ((10^9)*I26/PI()) * (16*2^(9/12)/($H$5*D26))^2 - 7,85*F26^2) / ALS(E26="i";$P$3;ALS(E26="m";$P$4;ALS(E26="k";$P$5;7,85))) + F26^2 )
Let ook hier weer op de toegevoegde 7,85 in de derde ALS()
Het kan zijn dat Excel moeilijk doet (= foutmelding geeft) over een niet ingevulde F26 = kern waarde in het geval geen i/m/k. In dat geval kan je de kern elke waarde, bv nul, geven, deze waarde valt toch automatisch weg in de formule (het gedeelte -kern^2+kern^2 onder de herschreven wortel).
Het alternatief is een zeer lange formule, waarin je onderscheid maakt tussen wel of geen i/m/k:
Tot =
ALS( OF(E28="i";E28="m";E28="k");
WORTEL( ( ((10^9)*I26/PI()) * (16*2^(9/12)/($H$5*D26))^2 - 7,85*F26^2) / ALS(E26="i";$P$3;ALS(E26="m";$P$4;$P$5)) + F26^2 );
WORTEL( ( (10^9)*I26/(7,85*PI()) ) * (16*2^(9/12)/($H$5*D26))^2 ) )
Indien er i/m/k gedefinieerd is, gebruikt Excel de eerste formule,
anders de gereduceerde formule met gamma_imk = 7,85.
Hierdoor voorkom je een #WAARDE foutmelding als Kern en i/m/k beide niet gegeven zijn.
Kom je hiermee verder?
Re: Hersenkraker! Wil werkende complexe formule omkeren
Ronduit geweldig!!
Ik ben begonnen met het invoeren van de aangepaste formule en tot nu toe werkt het perfect!!
Ook de variaties zijn nu makkelijker te herleiden door de andere opzet.
Zeer veel dank!
Mocht ik nog iets tegenkomen meld ik me weer hier
Ik ben begonnen met het invoeren van de aangepaste formule en tot nu toe werkt het perfect!!
Ook de variaties zijn nu makkelijker te herleiden door de andere opzet.
Zeer veel dank!
Mocht ik nog iets tegenkomen meld ik me weer hier

