In de eerste plaats ontzettend bedankt voor je uitgebreide reactie. Vooraleerst een paar opmerkingen over de antwoorden die je hebt gegeven op mijn vragen. De intuïtie achter de derde ERO (
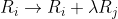
) is mij nu geheel duidelijk! Aangaande mijn vraag of het mogelijk is op grond van het gegeven dat twee stelsels dezelfde oplossingsverzameling hebben te besluiten dat ze rij-equivalent zijn, heeft je voorbeeld mijn vermoeden bevestigd. Beide matrices hebben dezelfde oplossingsverzameling ({ }), maar zijn niet rij-equivalent. Tot slot is mij nu ook duidelijk dat de begrippen rij- en kolomvector (of ook wel rij- en kolommatrix genoemd) alleen betekenis hebben in een matrixcontext.
arie schreef:
De pijl is een afbeelding: een variabele (links van de pijl) wordt afgebeeld op een functie van die variabele (rechts van de pijl).
)
Als je deze afbeelding A noemt, krijg je nog algemener:
)
De inverse afbeelding wordt dan
)
of zonder de afbeelding expliciet te noemen:
)
In het laatste geval zie je alleen niet dat dit de inverse afbeelding is van de eerste afbeelding hierboven. Dat zal je dan in de tekst moeten toelichten.
Over deze interpretatie heb ik echter nog een aantal vragen. Als hier inderdaad sprake is van een afbeelding, dan zou het gebruik van de afbeeldingspijl
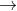
impliceren dat
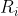
en
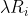
verzamelingen zijn, hetgeen natuurlijk niet het geval is. Als we er van uitgaan dat we
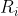
moeten opvatten als variabele (of element van het domein) en
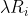
dus het beeld van
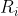
is onder

(conform jouw interpretatie), dan zou er toch eigenlijk gebruik moeten worden gemaakt van de beeldpijl
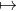
? Ook is
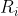
mijns inziens geen element van een verzameling (ofwel een variabele) omdat het geen vergelijking is. Tenzij er zoiets bestaat als een verzameling van alle vergelijkingen
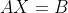
die we bv.

noemen (met
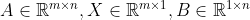
) (is dat überhaupt mogelijk?), maar dan zou de notatie
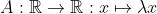
(met
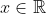
) toch veel logischer zijn?
Verder heb ik nog een aantal andere vragen. In het boek staat de volgende algebraïsche eigenschap van de vermenigvuldiging van matrices (onder voorwaarde dat
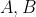
en
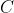
matrices zijn die telkens passende afmetingen hebben om bewerking uit te voeren):
A=A(\lambda I_{n}))
(ofwel, de vermenigvuldiging van een matrix met een scalaire matrix is commutatief). Maar volgens mij gaat deze commutativiteit alleen op als

een vierkante matrix is (die dan noodzakelijk dezelfde afmetingen heeft als de scalaire matrix). Is dit inderdaad het geval?
Daar ik mij afvroeg of de scalaire vermenigvuldiging met een matrix misschien een speciaal geval was van de 'gewone' scalaire vermenigvuldiging, ben ik eens nader gaan kijken naar wat vermenigvuldiging precies is. Zodoende kwam ik uit op het begrip operatie dat in zeer algemene termen gedefinieerd wordt als een procedure die uit één of meer invoerwaarden (operanden) een uitvoerwaarde produceert. Ik kwam de volgende formele definitie van een operatie als een afbeelding tegen
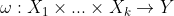
, maar deze formele definitie lijkt mij een stuk strikter dan de definitie in algemene termen. Een afbeelding is altijd een 'mapping' tussen de elementen van ten hoogste twee verzamelingen, maar de definitie in algemene termen lijkt te suggereren dat een operatie ook elementen uit verschillende verzamelingen kan koppelen aan één element uit een andere verzameling (codomein). Is dit inderdaad het geval? En zo ja, dan zou een operatie toch geen afbeelding kunnen zijn?
Als speciale gevallen van deze 'algemene' operaties worden de unaire en de binaire operaties genoemd (en daar vermenigvuldiging een binaire operatie is gaat mijn aandacht daar natuurlijk naar uit). De binaire operatie op bijvoorbeeld een verzameling
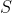
wordt formeel gedefinieerd als de afbeelding
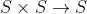
, we spreken dus alleen van een binaire operaties als de verzameling onder de operatie in kwestie gesloten is. Het domein van de operatie is dus altijd een cartesisch product van het codomein, de elementen waarop de binaire operatie wordt uitgevoerd en het element dat de output vormt komen allen uit dezelfde verzameling. Maar dit zou betekenen dat de scalaire vermenigvuldiging op
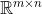
geen binaire operatie is, een scalair is immers geen matrix en dus geen
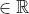
. Het zou volgens de formele definitie van een operatie zelfs helemaal geen operatie zijn, omdat een element gekoppeld wordt aan twee elementen uit verschillende verzamelingen (ofwel:
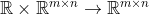
). Om gelijkaardige redenen voldoet ook het matrixproduct niet aan de strikte definitie van een binaire operatie (immers, voor
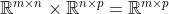
geldt hetzelfde). Hoe zit dit precies? En wanneer is een operatie nu precies wel of niet gedefinieerd op een verzameling?
Als bijkomende vraag nog het volgende, kan een verzameling ook gesloten zijn onder een partiële operatie? Een verzameling is immers gesloten onder een operatie als het toepassen van die operatie op elementen van die verzameling altijd weer een resulteert in een element diezelfde verzameling (hetgeen volgens mij dus betekent dat het domein altijd een cartesisch product is van het codomein, bv.
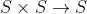
). In het geval van een partiële operatie kan immers niet aan elk element van
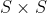
een element uit
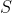
gekoppeld worden.
Tot slot nog een vraag over de betekenis van het woord rekenen in het algemeen. Wat verstaan we nu precies onder rekenen? Is het rekenen in bv.
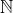
een 'verzameling' van alle unaire en binaire operaties op
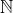
?
Het is al met al weer een lang betoog geworden en ik hoop dat ik mijn vragen duidelijk genoeg verwoord heb. Ik dank andermaal een ieder die de moeite neemt deze post te lezen en/of te beantwoorden.

