Beste mensen op het forum.
Ik heb de volgende vraag en de daarbij horende berekening, alleen weet ik niet of het antwoord klopt. Ik kan dit ook nergens terug vinden. Weten jullie het misschien?
Gegeven is het volgende stelsel vergelijkingen met parameter a:
x + 2y = 1
2x + a^2y = a
Bepaal alle a zodanig dat het stelsel
precies één oplossing heeft;
oneindig veel oplossingen heeft;
geen oplossing heeft.
Ik heb de matrix herschreven naar:
1 2 1
2 a^2 a
En toen naar
1 2 1
0 a^2 - 4 a - 2
Voor oneindig veel oplossing hoort de onderste rij alleen maar nullen te bevatten. Dus het antwoord daar is A=2
Voor geen oplossingen hoort er alleen een getal te staan in de laatste rij. Dus het antwoord daar is A=2 of A=-2
Alleen voor 1 oplossing weet ik het niet zo goed, is het dan elk getal behalve 2 of -2?
Ik hoop dat jullie mij kunnen helpen.
Matrix vraag.
Re: Matrix vraag.
Je had de matrix zelf correct herleid naar:

0*x + 0*y = 0
Dit is waar voor alle x en y, zodat alleen de eerste regel van je matrix overblijft:
1*x + 2*y = 1
Dit is het enige waar x en y aan moeten voldoen, en daarvoor zijn oneindig veel oplossingen.
Voor "geen oplossingen" zijn alle getallen op een regel nul, behalve het laatste!
Als a=2 krijgen we weer de situatie van hierboven: er zijn dan juist oneindig veel oplossingen.
Je kan dit inzien door bovenstaand stelsel te nemen:
[situatie 1]
als a=2 gaat het over in:

en zijn er oneindig veel oplossingen.
[situatie 2]
als a ongelijk aan 2 is, dan mogen we de laatste regel door (a-2) delen en krijgen we:

(bedenk dat a^2 - 4 = (a-2)*(a+2), een merkwaardig product).
[situatie 2a]
als in dit laatste geval a = -2, dan wordt de matrix

en zijn er geen oplossingen, want de laatste regel zegt:
0*x + 0*y = 1
en hiervoor bestaan geen oplossingen (x,y).
[situatie 2b]
als a nog steeds ongelijk aan 2 is en bovendien ook ongelijk aan -2 is,
dan mogen we de laatste regel ook door (a+2) delen:

Voor elke waarde van a heeft het stelsel nu precies 1 oplossing:
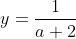
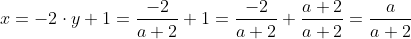
Klopt: een rij met alleen nullen komt overeen met de vergelijkingsvenster schreef: ... Voor oneindig veel oplossing hoort de onderste rij alleen maar nullen te bevatten. Dus het antwoord daar is A=2 ...
0*x + 0*y = 0
Dit is waar voor alle x en y, zodat alleen de eerste regel van je matrix overblijft:
1*x + 2*y = 1
Dit is het enige waar x en y aan moeten voldoen, en daarvoor zijn oneindig veel oplossingen.
Dit klopt niet:svenster schreef: ... Voor geen oplossingen hoort er alleen een getal te staan in de laatste rij. Dus het antwoord daar is A=2 of A=-2 ...
Voor "geen oplossingen" zijn alle getallen op een regel nul, behalve het laatste!
Als a=2 krijgen we weer de situatie van hierboven: er zijn dan juist oneindig veel oplossingen.
Klopt.svenster schreef: ... Alleen voor 1 oplossing weet ik het niet zo goed, is het dan elk getal behalve 2 of -2? ...
Je kan dit inzien door bovenstaand stelsel te nemen:
[situatie 1]
als a=2 gaat het over in:
en zijn er oneindig veel oplossingen.
[situatie 2]
als a ongelijk aan 2 is, dan mogen we de laatste regel door (a-2) delen en krijgen we:
(bedenk dat a^2 - 4 = (a-2)*(a+2), een merkwaardig product).
[situatie 2a]
als in dit laatste geval a = -2, dan wordt de matrix
en zijn er geen oplossingen, want de laatste regel zegt:
0*x + 0*y = 1
en hiervoor bestaan geen oplossingen (x,y).
[situatie 2b]
als a nog steeds ongelijk aan 2 is en bovendien ook ongelijk aan -2 is,
dan mogen we de laatste regel ook door (a+2) delen:
Voor elke waarde van a heeft het stelsel nu precies 1 oplossing:

