Wiskundeforum

Ik vroeg me af hoe je dit kan bewijzen:

"Een transformatie die iedere basis op een andere basis afbeeldt voor alle mogelijke vectorruimten is heeft een matrix van de vorm ."



In de omgekeerde volgorde is dit makkelijk in te zien, maar ik geraak er maar niet aan uit. Kan iemand mij een aanzet geven?

De stelling kan eigenlijk echt niet kloppen.
Want neem bijvoorbeeld een lineaire transformatie in een willekeurig dimensionale vectorruimte die de eerste twee coördinaten met een hoek van 90°draait, en de andere coördinaten hetzelfde houdt.
Dan is eenvoudig in te zien, dat als twee vectoren lineair onafhankelijk zijn in de domein-vectorruimte ze dit ook zijn in de beeld-vectorruimte, en de dimensie moet ook altijd hetzelfde zijn van het doel als van het beeld, aangezien de kern triviaal is, en het aantal vectoren blijft ook gelijk dus heb je een maximaal vrij deel a.k.a. een basis.

Of heb ik niet helemaal mee wat de vraag was, want die was een klein beetje verwarrend.

Sorry, ik bedoelde "alle mogelijke deelruimten".

Aha, nu denk ik dat het helemaal duidelijk is.

Dus ik denk dat elke deelruimte ook op zichzelf moet worden afgebeeld, omdat dat de enige mogelijkheid is waarop een basis van die deelruimte nog steeds een basis blijft van die deelruimte. (Stel dat dit niet zo is, neem dan een vector in de deelruimte waarvan het beeld niet in deze deelruimte zit, vul dit aan tot een basis, en dan is het beeld onmogelijk een basis van de deelruimte. Het beeld van de deelruimte kan ook geen strikte deelverzameling zijn van de deelruimte zelf, want dan is de kern niet triviaal, en is er dus een vector die als beeld de nulvector heeft, vul deze vector aan tot een basis, en dan is het beeld onmogelijk vrij, dus geen basis.)

Dus hieruit kan al worden afgeleid dat ten opzichte van een will. basis, de matrix een diagonaalmatrix is. Want het beeld van de deelruimte voortgebracht door een basisvector is telkens de deelruimte zelf, dus is het beeld van deze basisvector lambda keer de basisvector zelf, wat resulteert in allemaal nullen in deze kolom buiten op de plaats van de diagonaal.
Elke vector moet ook een eigenvector zijn. (stel dat een vector dat niet is, neem dan de deelruimte voortgebracht door deze vector, dan is het beeld van deze deelruimte niet de deelruimte zelf, omdat het beeld van deze vector niet in de vectorruimte zit.)

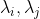
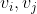
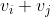
stel dat er twee lambda's verschillend zijn neem bijvoorbeeld de lambda's horende bij dan is wat enkel een veelvoud is van als deze twee lambda's gelijk zijn, maar dat zijn ze dus niet, wat tot een contradictie leidt.

Er moet wel nog lambda=0 uitgesloten worden, om obvious reasons.

aha, zo gaat dat dus.
Bedankt!