Mijn vraag is als volgt:
dus;
Hoe kom ik in dit geval aan x?
Ik heb hier al een paar uur tegenaan gehikt en krijg hem niet opgelost.
Dit is geen verg maar een functie, dwz voor iedere x vind je een y.Kikker schreef:Mijn vraag is als volgt:
dus;
Hoe kom ik in dit geval aan x?
Ik maak hier wel de volgende kanttekening.Kikker schreef: Ik mijn boek stond het volgende:
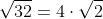
Wat ik deed voor 2^20 is het volgendeKikker schreef:De basis voor 2 ken ik tot de macht 16 uit mijn hoofd (65 536, daarna wordt het te veel).