Ongelijkheid en absolute waarde
Re: Ongelijkheid en absolute waarde
Het eerste deel is immers waar voor alle x<0 ... , en dat interval was nog niet aan de orde gekomen!
Re: Ongelijkheid en absolute waarde
Dit heeft betrekking op jou laatste post? Want dat begint, voor mij, wel erg lastig geworden. Je heb immers de absolute waarde weer teruggebracht. Mijn taak hier is om van die dingen af te komen.SafeX schreef:Het eerste deel is immers waar voor alle x<0 ... , en dat interval was nog niet aan de orde gekomen!
Safex is mijn oplossing uit mijn vorige post fout dan? Is die oplossing misschien acceptabel op mijn niveau? Voor de duidelijkheid ik werk zelfstandig door het basisboek wiskunde. Dit alles is erg nieuw voor mij.
Nog een vraag: Ik kan geen voorbeelden van dit soort opgaven vinden met Google. Heb je misschien wat zoektermen voor mij? "Inequalities and absolute value" geeft mij alleen maar voorbeelden van lineaire problemen.
Re: Ongelijkheid en absolute waarde
Algemeen: Ongelijkheden moeten voor de gehele R worden opgelost.
Absolute waarde en eveneens de wortel dwingt tot het opsplitsen van R.
Voor de absolute waarde kan je ook schrijven (in dit geval): x<0 en |1-x|=1-x, maar er is geen enkele reden om dat ook te doen ...
Absolute waarde en eveneens de wortel dwingt tot het opsplitsen van R.
Voor de absolute waarde kan je ook schrijven (in dit geval): x<0 en |1-x|=1-x, maar er is geen enkele reden om dat ook te doen ...
Re: Ongelijkheid en absolute waarde
Hallo Safex alvast bedankt voor het engelengeduld dat je getoond hebt. Maar ik kom er helaas niet uit aan de hand van jou opmerkingen. Wil jij misschien de eerste twee regels van de correcte uitwerking posten zodat kan leren door imitatie??SafeX schreef:Algemeen: Ongelijkheden moeten voor de gehele R worden opgelost.
Absolute waarde en eveneens de wortel dwingt tot het opsplitsen van R.
Voor de absolute waarde kan je ook schrijven (in dit geval): x<0 en |1-x|=1-x, maar er is geen enkele reden om dat ook te doen ...
Re: Ongelijkheid en absolute waarde
Je hebt nu de gehele oplossing ... , dus als je nog ergens een vraag over hebt is het belangrijk dat je zo nauwkeurig mogelijk dat aan geeft.
Ik merk niet dat je iets 'doet' met wat ik heb aangegeven ...
Je hebt de grafiek, wat is volgens de grafiek je oplossing?
Ga na dat de intervallen waarin R is opgedeeld tot die oplossing leiden.
Ik merk niet dat je iets 'doet' met wat ik heb aangegeven ...
Je hebt de grafiek, wat is volgens de grafiek je oplossing?
Ga na dat de intervallen waarin R is opgedeeld tot die oplossing leiden.
Re: Ongelijkheid en absolute waarde
Okay, dan ga ik nog even mee aan de slag! Ik probeer overigens al jou hints en opmerkingen wel degelijk te gebruiken. Maar in dit geval 'klikt' het niet. Bedankt voor de moeite!SafeX schreef:Je hebt nu de gehele oplossing ... , dus als je nog ergens een vraag over hebt is het belangrijk dat je zo nauwkeurig mogelijk dat aan geeft.
Ik merk niet dat je iets 'doet' met wat ik heb aangegeven ...
Je hebt de grafiek, wat is volgens de grafiek je oplossing?
Ga na dat de intervallen waarin R is opgedeeld tot die oplossing leiden.
Re: Ongelijkheid en absolute waarde
Nogmaals geef dat precies aan ...Eddy schreef:Ik probeer overigens al jou hints en opmerkingen wel degelijk te gebruiken. Maar in dit geval 'klikt' het niet.
Re: Ongelijkheid en absolute waarde
Hier zat nog een foutje in. Zie de post hieronder.
Laatst gewijzigd door Eddy op 04 mar 2013, 16:36, 1 keer totaal gewijzigd.
Re: Ongelijkheid en absolute waarde
Bijna,
2.1)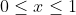 :
:
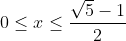
Je begint met een voorwaarde en je gebruikt die niet in je conclusie:2.1) Interval:
wordt
;
na sorteren;
na uitwerken. Dit is dus het tweede deel van de oplossing.
2.1)
Re: Ongelijkheid en absolute waarde
Nogmaals, nu goed:
Gegeven: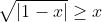
1) De ongelijkheid is altijd waar voor de interval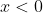 . Dus het eerste deel van de oplossing is
. Dus het eerste deel van de oplossing is 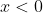 .
.
2) Voor de interval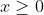 mag ik kwadrateren. Dat geeft:
mag ik kwadrateren. Dat geeft: 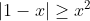 . Het kritieke punt van de absolute waarde uitdrukking is
. Het kritieke punt van de absolute waarde uitdrukking is 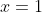 dus nu bekijk ik de gevallen
dus nu bekijk ik de gevallen 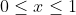 en
en  .
.
2.1) Interval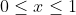 :
:
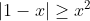 wordt
wordt  ;
;
 na sorteren;
na sorteren;
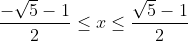 na uitwerken. Combineren met de voorwaarde geeft:
na uitwerken. Combineren met de voorwaarde geeft: 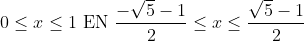 . Dat ik samenneem tot:
. Dat ik samenneem tot:  en dat is het tweede deel van de oplossing.
en dat is het tweede deel van de oplossing.
2.2) Interval :
:
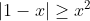 wordt
wordt 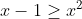 ;
;
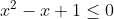 na sorteren. Deze ongelijkheid heeft geen oplossing. Dat is dan het derde deel van de oplossing.
na sorteren. Deze ongelijkheid heeft geen oplossing. Dat is dan het derde deel van de oplossing.
Nu voeg ik alle drie oplossingen samen: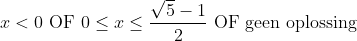 . Dit kan ik samennemen tot
. Dit kan ik samennemen tot 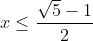 en dat is de oplossing.
en dat is de oplossing.
Gegeven:
1) De ongelijkheid is altijd waar voor de interval
2) Voor de interval
2.1) Interval
2.2) Interval
Nu voeg ik alle drie oplossingen samen:

