Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Het forum voor overige vragen betreffende wiskunde uit het hoger onderwijs.
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 17 sep 2014, 18:05
ik ben echt een knoeier hoor. vandaag weer bezig geweest maar kom er wederom niet uit. Maar ik wil het gewoon kunnen. ergens zweeft de oplossing in mijn hoofd maar ik krijg het niet te pakken. Als ik een voorbeeld heb hoe ik het verder moet uitwerken gaat het wel lukken maar het boek schiet even tekort bij deze opgave.
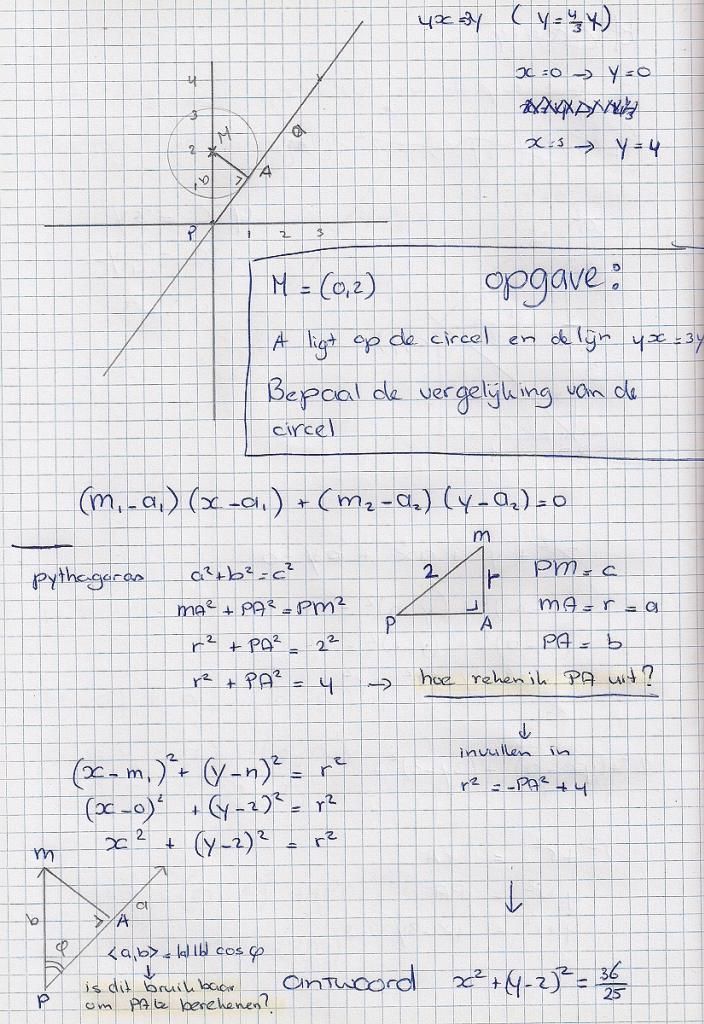
als ik weet hoe ik PA uitreken gaat het me wel lukken maar ik loop helemaal vast denk dat het via de vectoren moet ( linksonderin) er was ook nog iets dat ax+by =c maar daar loop ik vast op de c.
mvgr Ellen
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 17 sep 2014, 18:06
er is een stuk van de afbeelding weggevallen zie ik. ga ik nog even in orde maken
zie dat er een maximale breedte geld in dit forum. rechtsklikken en openen in nieuw venster toont de afbeelding in zijn geheel.
mvgr Ellen
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 17 sep 2014, 18:57
Ben je met me eens dat je alleen maar de straal nodig hebt, dus MA?
Heb je formule voor de afstand van een punt tot een lijn geleerd?
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 17 sep 2014, 19:04
mijn probleem is het vinden de van coötdinaten van A (ik kom er dus niet uit om die coördinaten te vinden maar dat zou dan met de formule die gegeven was moeten, de forumule onder de grafiek is de formule uit de begeleidende tekst die het onderwerp raaklijnen aan een circel introduceert maar die krijg ik niet uitgerekent wegens teveel onbekenden.
mvgr Ellen
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 17 sep 2014, 19:08
de clou moet dus zitten in de formule
(M1 - A1)(X - A1)+(M2-A2)(Y-A2)=0
maar A1 en A2 kan ik niet berekent krijgen
mvgr Ellen
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 17 sep 2014, 19:26
Bedenk dat MA loodrecht op de lijn staat. Omdat je de vergelijking van de lijn kent weet je ook hoe de coördinaten van A met elkaar samenhangen. Probeer aan de hand hiervan eens verder te gaan.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 17 sep 2014, 19:48
Is de gegeven lijn 4x=3y?
ceitwa schreef:de clou moet dus zitten in de formule
(M1 - A1)(X - A1)+(M2-A2)(Y-A2)=0
maar A1 en A2 kan ik niet berekent krijgen
Weet je wat deze verg voorstelt? Wat heb je daarvan geleerd?
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 18 sep 2014, 19:43
ik ben daar nog niet precies uit.
wat ik wel in mijn hoofd heb is de vergelijking van een lijn
Y=aX + b dat zou hier zijn Y= 4/3X +0
de lijn die daar door de oorsprong loodrecht mee kruist is
Y= -3/4X + 0 en omdat M is (0,2) moet die lijn omhoog b=2
als ik die twee terugschrijf
4X - 3Y = 0
-3X + 4Y - 8=0 kan ik dan punt A uitrekenen? en die invullen voor a1,a2 of moet ik de coordinaten van het middelpunt juist nemen voor a1, a2
mvgr Ellen
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 18 sep 2014, 20:05
4x= 3y is de formule van de raaklijn.
de tekst in mijn boek is
Als M= (m1,m2) het middelpunt van een circel is en A=(a1,a2) is een punt op die circel, dan is de vergelijking van de raaklijn aan de circel in A
(m1 -a1)X + (m2-a2)Y = (m1 -A1)a1 + (m2-a2)a2
en die vergelijking is gelijk aan:
(m1-a1)(X-a1) + (m2-a2) (Y-a2)=0
m1=0
m2=2
en de anderen weet ik niet en loop ik op vast
mvgr Ellen
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 18 sep 2014, 20:58
hoe langer ik er mee bezig ben hoe minder ik het snap...
kan het antwoord in het boek fout zijn? ik kan nergens die 5 terugvinden

(vanuitgaande dat 36/25 dus rkwadraat is 6/5)
antwoord volgens boek is X^2 + (y - 2)^2 = 36/25
mvgr Ellen
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 18 sep 2014, 22:21
Ok, laat eens zien wat je nu kunt opschrijven...
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 19 sep 2014, 08:38
Een aanzet ...
verg raaklijn door A: (0-a1)x+(2-a2)y=(0-a1)a1+(2-a2)a2 (*)
deze raaklijn heeft ook de verg: 4x-3y=0
Nu mag je (natuurlijk) niet zeggen dat bv -a1=4. Eens?
Maar deze verg kan je ook schrijven als: 4kx-3ky=0 voor alle k ongelijk 0. Eens?
Wat kan je nu wel opschrijven ... ?
Vraag: moet je verg (*) uit het hoofd kennen?
Opm: ik ben nu verder gegaan met jouw methode, maar het kan wel eenvoudiger. Bedenk dat je nu (a1,a2) bepaalt terwijl je r zoekt ...
Daar zal ik later (als je dat wilt) op terugkomen!
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 19 sep 2014, 17:47
ziet er logisch uit. Nee ik hoef voorlopig niks uit mijn hoofd te kennen. is pure zelfstudie omdat ik volgend jaar aan de opleiding docent natuurkunde (tweede graad) mag gaan beginnen. Ik hoop door het nu te snappen straks meer tijd aan de didactische vakken en natuurkunde zelf te kunnen besteden. Heb geen idee of ik het dan nodig heb maar ik werk het boek van begin tot einde door.. Wellicht grijp ik zelfs hoger dan nodig. Maar ik vind het aha moment iedere keer geweldig als ik mijn denkfout kwijt ben... en door zelf hier mee te zwoegen kan ik me straks denk ik beter in mijn studenten verplaatsen als ze ergens de logica niet van inzien.

mvgr Ellen
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 19 sep 2014, 18:55
is de k bij 4kx dezelfde als die bij 3ky?
ik zat inmiddels meer te denken in gebruik maken van de abc formule en dan met name de discriminant die gelijk aan 0 moet zijn met gebruik van ax+by = c
weet even niet hoe ik dit moet opschrijven maar het snijpunt bepalen van x^2+(y-2)^2 en 4x-3y door x te vervangen door 3/4 y moet ik dan ook nog die k factor gebruiken? dus dan 3/4ky invullen?
ik zoek inderdaad r maar denk dat als ik deze als vector zie die begint in (a1a2)en eindpunt M heeft die kan berekenen. maar als er een andere manier graag wellicht zit mijn denkfout daar. mijn doel is het te kunnen berekenen ook als het evt anders gaat dan de in het boek gegeven manier die voortborduurt op de tekst.
mvgr Ellen
-
ceitwa
- Vast lid

- Berichten: 60
- Lid geworden op: 18 aug 2014, 19:23
- Locatie: Zuid Beveland
-
Contacteer:
Bericht
door ceitwa » 19 sep 2014, 20:00
via onderstaande forumules ben ik trouwens naar deze opgaven geleid waar de onderste degenen zijn die ik nu zou moeten toepassen om de opgaven te maken.

mvgr Ellen













