Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Het forum voor overige vragen betreffende wiskunde uit het hoger onderwijs.
-
1990
- Gevorderde

- Berichten: 115
- Lid geworden op: 27 apr 2009, 08:50
Bericht
door 1990 » 24 mei 2015, 16:59
Hoi allemaal,
Uit het volgende sommetje kom ik helaas niet uit. Wat zijn de logische stappen om s te bepalen?
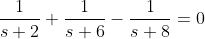
Het antwoord is:
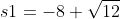
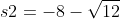
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 24 mei 2015, 18:08
1990 schreef:Hoi allemaal,
Uit het volgende sommetje kom ik helaas niet uit. Wat zijn de logische stappen om s te bepalen?
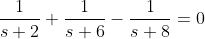
De eerste stap is om de breuken gelijknamig te maken. Zorg er voor dat iedere breuk de noemer (s+2)(s+6)(s+8) heeft. De volgende stap is dat je de breuken samenneemt zodat je slechts 1 breuk met noemer (s+2)(s+6)(s+8) overhoudt. Tenslotte gebruik je de eigenschap dat een breuk alleen maar nul kan zijn als de teller nul is. Daaruit bepaal je de gezochte waarde(n) voor s.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 24 mei 2015, 21:31
Waar komt de opgave vandaan?
Wat heb je zelf al geprobeerd ...
-
1990
- Gevorderde

- Berichten: 115
- Lid geworden op: 27 apr 2009, 08:50
Bericht
door 1990 » 24 mei 2015, 22:21
arno schreef:1990 schreef:Hoi allemaal,
Uit het volgende sommetje kom ik helaas niet uit. Wat zijn de logische stappen om s te bepalen?
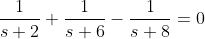
De eerste stap is om de breuken gelijknamig te maken. Zorg er voor dat iedere breuk de noemer (s+2)(s+6)(s+8) heeft. De volgende stap is dat je de breuken samenneemt zodat je slechts 1 breuk met noemer (s+2)(s+6)(s+8) overhoudt. Tenslotte gebruik je de eigenschap dat een breuk alleen maar nul kan zijn als de teller nul is. Daaruit bepaal je de gezochte waarde(n) voor s.
Dank voor de heldere uitleg.
-
1990
- Gevorderde

- Berichten: 115
- Lid geworden op: 27 apr 2009, 08:50
Bericht
door 1990 » 24 mei 2015, 22:24
SafeX schreef:Waar komt de opgave vandaan?
Wat heb je zelf al geprobeerd ...
De opgave komt uit het boek: regeltechniek voor het hbo.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 25 mei 2015, 08:27
Had je wel (bv) de eerste twee breuken kunnen optellen ...
-
1990
- Gevorderde

- Berichten: 115
- Lid geworden op: 27 apr 2009, 08:50
Bericht
door 1990 » 25 mei 2015, 09:50
SafeX schreef:Had je wel (bv) de eerste twee breuken kunnen optellen ...
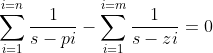
Hierin is pi de polen van het systeem (die zitten altijd in de noemer van het gegevens systeem). En zi de nulpunten van het systeem (die zitten altijd in de teller van het gegeven systeem). n is het aantal polen in het systeem. En m is het aantal nulpunten in het systeem.
Gegeven systeem:
 = K\frac{2+8}{(s+2)(s+6)})
Hierin is er één nulpunt (m=1), namelijk in z1=-8 . En twee polen (n=2), namelijk p1=-2 en p2=-6.
Met de bovenste formule kunnen de plaats van de vertrek- en aankomstpunten worden berekend van het systeem. Als je die formule invult krijg je de breuknotatie die in mijn eerste post staat. Volgens mij mag 1/(s+2) en 1/(s+6) met elkaar worden opgeteld, maar ik weet het niet zeker. Ik weet niet hoe je de noemers dan gelijk krijgt.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 25 mei 2015, 10:01
1990 schreef:
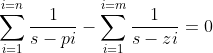
Klopt dit, want nu zijn de zi ook polen en geen nulptn ...
Hoe tel je het volgende op:
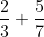
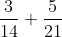
-
1990
- Gevorderde

- Berichten: 115
- Lid geworden op: 27 apr 2009, 08:50
Bericht
door 1990 » 25 mei 2015, 15:40
SafeX schreef:1990 schreef:
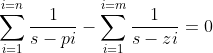
Klopt dit, want nu zijn de zi ook polen en geen nulptn ...
Hoe tel je het volgende op:
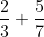
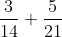
Hoe die formule is afgeleid weet ik niet, dat staat ook niet in het boek. Maar ik neem aan dat die juist is.
Noemers gelijk maken en dan optellen

uit de eerste komt 29/21
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 25 mei 2015, 17:16
En de tweede ...
Ik vraag dit omdat dit heel elementair is en waarvan ik mag verwachten dat je daar geen moeite mee hebt, de regels waarmee je werkt blijven natuurlijk ook met letters geldig ...
-
1990
- Gevorderde

- Berichten: 115
- Lid geworden op: 27 apr 2009, 08:50
Bericht
door 1990 » 25 mei 2015, 18:21
SafeX schreef:En de tweede ...
Ik vraag dit omdat dit heel elementair is en waarvan ik mag verwachten dat je daar geen moeite mee hebt, de regels waarmee je werkt blijven natuurlijk ook met letters geldig ...
Ik zou hem zo doen:
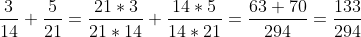
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 25 mei 2015, 19:17
1990 schreef:Ik zou hem zo doen:
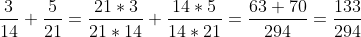
Dat is veel te omslachtig. Merk op dat 21 en 14 ieder een factor 7 bevatten, dus dat je kunt schrijven dat
)
. Maak nu eerst eens de breuken tussen haakjes gelijknamig. Wat kun je dus schrijven voor
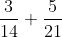
?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
1990
- Gevorderde

- Berichten: 115
- Lid geworden op: 27 apr 2009, 08:50
Bericht
door 1990 » 26 mei 2015, 20:55
arno schreef:1990 schreef:Ik zou hem zo doen:
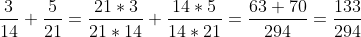
Dat is veel te omslachtig. Merk op dat 21 en 14 ieder een factor 7 bevatten, dus dat je kunt schrijven dat
)
. Maak nu eerst eens de breuken tussen haakjes gelijknamig. Wat kun je dus schrijven voor
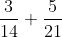
?
Ja inderdaad, dit vereenvoudigt de breuk meer.
=\frac{1}{7}\left(\frac{9}{6}+\frac{10}{6}\right)=\frac{1}{7} \cdot \frac{19}{6}= \frac{19}{42})
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 26 mei 2015, 21:03
Ok, al had ik liever dat je dat zelf gevonden had ...
Hoe ga je nu verder te werk ...

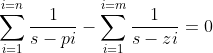
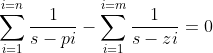

. Maak nu eerst eens de breuken tussen haakjes gelijknamig. Wat kun je dus schrijven voor
?