zegt ons:
Dus
zegt ons:
Toch(?!!)
De notatie,
Maar dat zal wel tegen oude gewoonten ingaan.
Nee, er is een groot verschil tussen een reeks en zijn limiet.David schreef:Ok dank je, als het aantal termen van een rij die opgeteld een reeks vormen, is de afspraak:
Maar je laat zelf de index beginnen bij k=0, je bronnen bij k=1. Is daar nog verschil in afspraak?
Dit stuk begrijp ik niet helemaal. Een reeks is een verkorte schrijfwijze voor een rij?op=op schreef: Bijv.is een reeks (geen getal), d.w.z. het is een verkorte schrijfwijze voor de rij 1!, 1!+2!, 1!+2!+3!, ...
Taalkundig is er nauwelijks of geen verschil tussen de begrippen rij en reeks.David schreef:Dit stuk begrijp ik niet helemaal. Een reeks is een verkorte schrijfwijze voor een rij?op=op schreef: Bijv.is een reeks (geen getal), d.w.z. het is een verkorte schrijfwijze voor de rij 1!, 1!+2!, 1!+2!+3!, ...
Is de volgende zijn juist:
"Een rij sommeert tot een reeks"?
Omdat elk element n van de rij de som is van de eerste n elementen van de "vorige" rij, wordt de rij ook een reeks genoemd. Omdat de waarde van de reeks convergeert, "naar een getal toe gaat," heeft de rij een (eindige!) limiet.op=op schreef: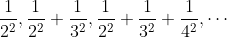

Volgens deze definitie isSjoerd Job schreef: Merk tevens op dat de notatie
ook om een soortgelijke definitie vraagt. Meestal wordt
gekozen.

Vind ik wel een betere definitie. Uiteraard is het zo dat als de beide limieten bestaan, de waarde gelijk is aan de def die ik gaf..op=op schreef:Volgens deze definitie isSjoerd Job schreef: Merk tevens op dat de notatie
ook om een soortgelijke definitie vraagt. Meestal wordt
gekozen.
,
hetgeen tegen mijn haren instrijkt.
Meer naar mijn smaak is de definitie
mits de limieten in het rechter lid bestaan.
(Voor ingewijden: In topologische ruimten kennen we een generalisatie van het begrip rij, n.l. het net. Netten kunnen convergeren en divergeren).
Die zou ik niet te snel gebruiken.Sjoerd Job schreef:Merk tevens op dat de notatie
ook om een soortgelijke definitie vraagt. Meestal wordt
gekozen.
Hoe is dieDavid schreef: Ik zou voor
gaan.